首先我们一定一定要知道，对于参数化设计，参数实在是太重要了，没有参数的参数化不是好厨子。既然是参数，绝不是我们小学学的1+1=2这样的简单的一维数组（这个东西都称不上数组…）
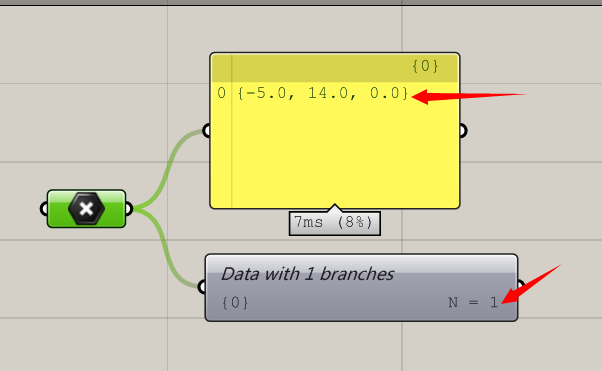
那么对应的，最简单的参数结构，我称之为一维数（树）形结构。我用point随手画了个点，它的数据结构如下。其中panel的数据是在{0}分组里，共有一个点，坐标给标了出来，同时下边的英文是，数据只有一个分支，Number=1，意思是在这个分支下有一个数据（一个点）

那么我们用两个点来试一下看看会有什么变化。这两个点被shift链接到panel以后，自动放在了{0}这一组，下边显示两个点的坐标。那么这两个点如果我们用Point Display来看的话，他们的名字分别叫做0，1，并且颜色一定是一样的。一个颜色代表一个分组{0}，这就相当于是表兄弟，都姓Jin，一个叫Daniel，一个叫Fxxk，也许他们差几岁，但是DanielJin和FxxkJin是一个辈分的。
这里要注意的是结构类型显示框不能被多个输出链接，所以我做了两个，一个是英文，一个是直接用形状表示了树形结构的情况。这个会在后边看的更清楚明白。

接下来我们给这两个点拾取器设置多个点，set multiple points，大家首先可以注意到，单线变成了空心的双线，代表输出了多个数据。在这里大家可以清楚地看到在一个分组{0}里出现了0-5共6个点，其中一个拾取器后边的Number=3，每一个点了三个点，他们的树形结构还是一样的，数据类型都是在{0}分组里，同一辈分。

接下来我们做一个稍微不同的生成点的方式，我们用随机点阵生成了一百个点。大家可以注意到，这些组被自动分在了{0,0}里，在树形结构图上可以看得很清楚从绿色的原点（source point）出发，经过第二级分组变成了红色，但是还是一个分组。这些分组从刚才的{0}变成了{0,0}二级分组，就相当于现在来了一百个孙子，是下一辈的。但是其实这个第二级分组是个无效分组，我也不清楚gh为何会在多数据的情况下自动加一个无效分组，但是从之后的例子来看，数据一定是加了一个无效分组的。
什么叫无效分组？就是在这一级里，只有这一组，没有{0,1}这样的分组，为了简化其实可以将这一组往上提一下级别，山中无老虎猴子当霸王的感觉。当然这只是我个人的习惯为了看数据简单，因人而异。不过我还是推荐你这么做，因为后边的例子能充分告诉你不简化分组将会有如何恐惧的树形结构出现。

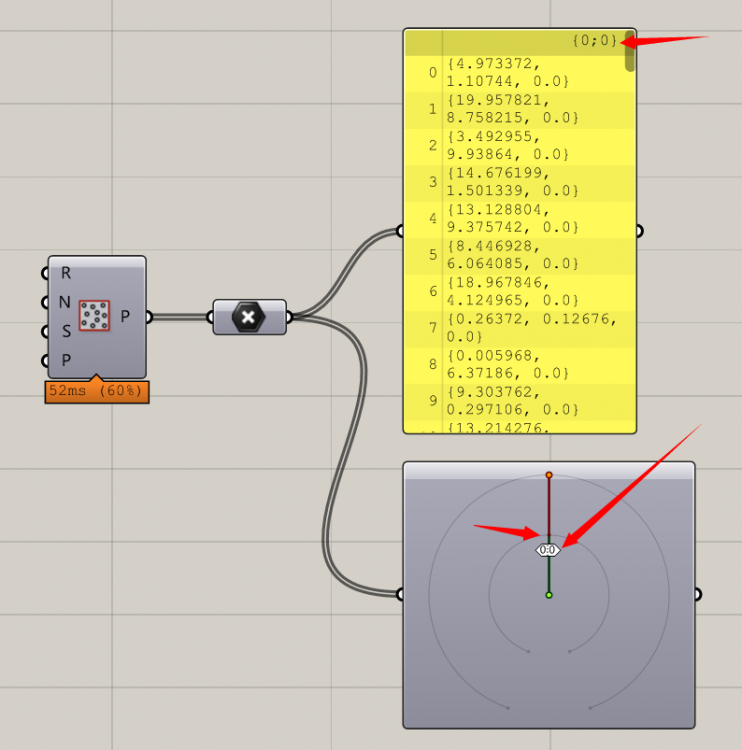
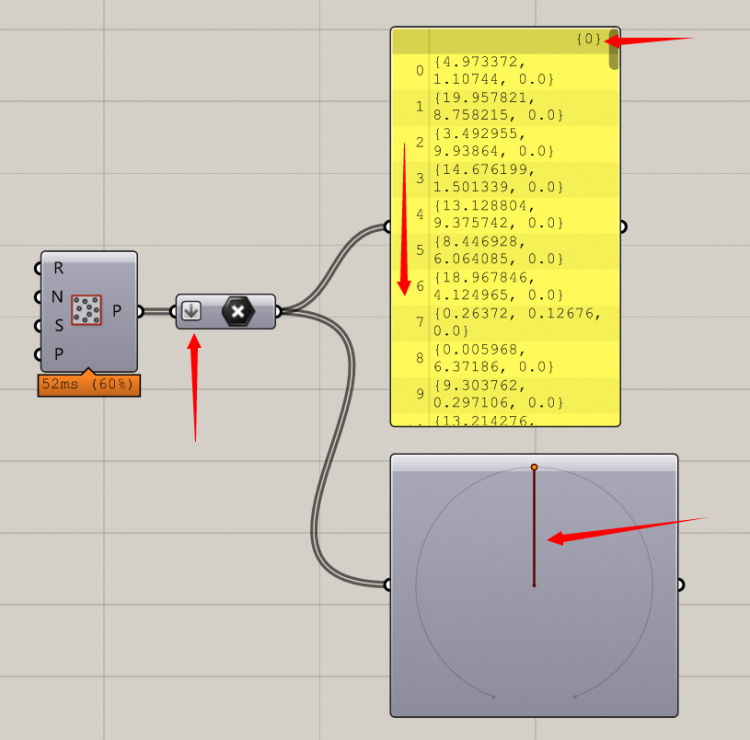
我们将刚才的例子分组简化（拍平），点依旧按照我们熟悉的方式在{0}组里依次从0到了99.孙子都长大了打怪升级了。

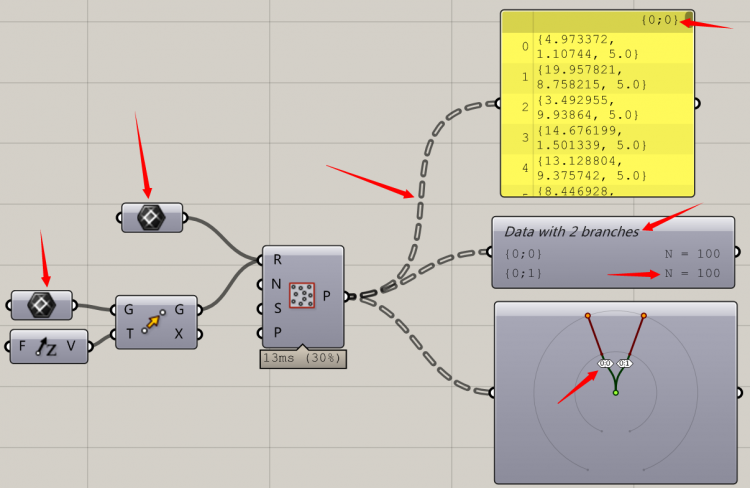
由于随机点阵是要在一个矩形内生成的，我们之前用的是默认的矩形，现在我们把这个默认的矩形提取出来，同时再往上移动一定的距离出现第二个矩形。这时候我们看到输出的点变成了虚线，这就是典型的gh的树形结构的线，大家可以看到这时候的分组变成了{0,0}这样，这时候我就不将其成为无效分组了，为什么呢，大家可以看得很清楚，数据被分成了两个枝干，每个枝干N=100有100个数。从resource point直接分叉，变成了两组数据。大家可以看到两个圆弧，每一道就代表一个分级点。这时候如果你想选择上边矩形的点你就要用相应的运算器选择相应的{0,1}组，然后进行编辑。如果我们还按照刚才的方式拍平，你只能手动选择后一百个点，非常麻烦。这就是分组的好处之一。

那么我们在复杂一点，我们拿出一个随机运算器，将范围设定为1-4，等分成十分（相应生成11个分割点），在此时这些点的数据还是一组的。虽然是孙子辈的，但是你可以理解为无效数据。这一辈的人和同级别的random运算器繁衍生出来的孩子一定是曾孙子辈的，对吗？我们看一下，我们得到了下一组数据的分组是11个分支，从resource point出发以后到第二个绿色的点（同级别resource point，相当于孩子的妈妈）开始进行下一组分支，共得到了11个枝干。分别对应{0,0,0}到{0,0,10}。细心地朋友会发现在每一组里，每个点的序号都是0，我们如果用display看的话将会有11种颜色的点，每个颜色只有一个点。我们刚说过，在上一组中有一级别的无效分组，还记得吗？因此这一级别中一定有一等级的分组是无效的。我们可以试想一下如果我们把random或者之前的range拍平，出来的结果一定是{0,0}到{0,10}的分组，并且每一组的点名字还是0。我们可以试一下。

拍平以后，和我们预计的结果一样对吗？

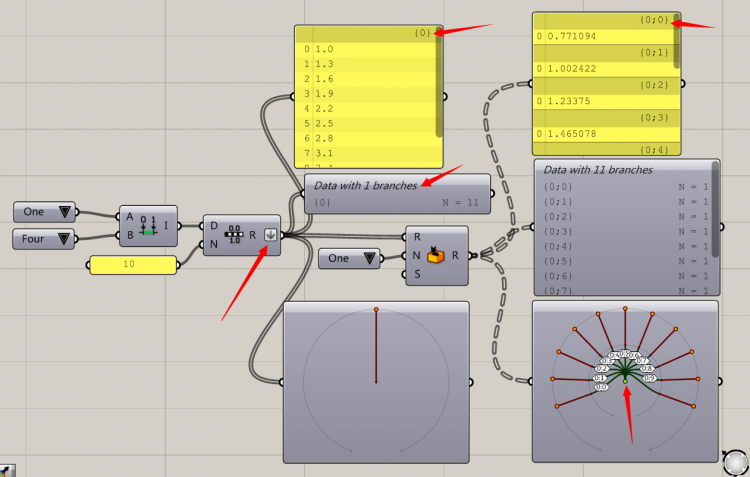
接下来我们不但不拍平，我们将random再分一次组，我们可以看到树形数据的结构越来越华丽了。细心地朋友又会发现了，为什么是44个分支呢？刚才是11个分支，我们的random N=4，因此在右上角可以看到，0,1,2,3循环以后自动分了一组，括号内的十位数吧（暂且这么称呼）变成了1，同理4个数字以后变成了2.像不像10进制计数法，2进制计数法？我们自己创造了4进制计数法。

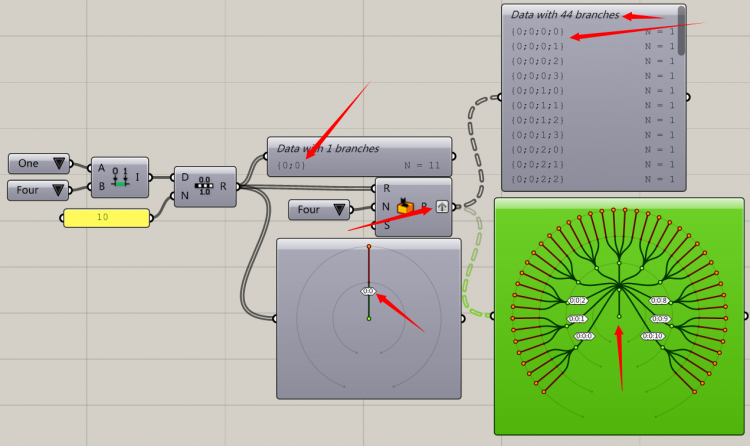
由于graft只能加一个分组，所以我们加一个graft运算器来再增加一次分组，这时候大家会发现，数据仍然是44个分组，只不过分组变化的0123排序后又增加了一个0，我们暂且成为小数点之后增加了个0吧。我们都知道1=1.0的，因此即使我们再增加一次分组，仍然将会是44个分支，不再变化。这就相当于我们的子孙已经绝育了，数据实在已经分完了没有下一代了。其实这时候的小数点0才是真正的无效分组，这是我们强加上去的，yy上去的。刚才我们说的无效分组，在某些时候还是有用的。比如我们可以用合并运算器加入一个{0,1}的组进去，这样刚才的{0,0}就不能再称之为无效分组了。听晕了吗？如果我们有{0,0}（我们成为复姓吧，比刚才的姓0多了一个字）分组下的100个点，我们又加入复姓{0,1}的100个点，那么这两个大家族的存在，就让我们的复姓{0,0}变得有意义了。如果部落里只有南宫萨尔（Lok’tar ogar!!），南宫阿尔萨斯这两个人，我们自然可以简称为萨尔和阿尔萨斯。可是如果部落里又来了欧阳吉安娜，那么我们为了避免混淆就要叫萨尔全名了。当然这样分组的好处是，如果我们去掉这一个复姓分组，三人同等级无法相交发生关系。如果加入复姓，三人则成为两组可以分别和吉安娜…我们经常见到这样的运用，比如一张表皮离中心点越远开洞越小，就是同数量的欧阳组的数据影响了南宫组的半径从而导致了开洞面积发生变化。

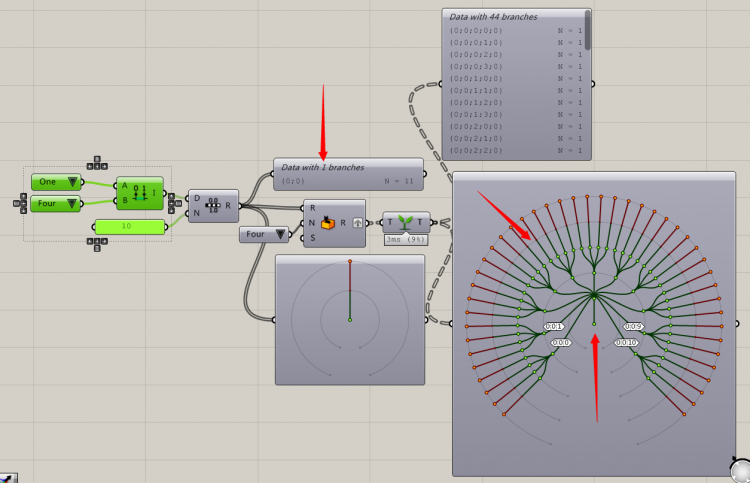
那么初级部分的数据类型介绍到此就算告一段落了。在中级部分我们还会推出十分全面的深刻的数据分组专门的理论贴。

最后，小黄人君想上两张图，这两张图我很感动。这是一个大二的学妹跟着我的教程走，然后觉得不够自虐，又去找了王大川老师的参数化建模这本书一点点啃，认认真真学习的时候我拿她笔记拍的照片。她才大二，不允许计算机出图还在手绘阶段，你几岁？如果你是拥有这样态度的新手，我告诉你我的手机你可以24小时骚扰我我会向你答疑。因为我会从内心尊重你。

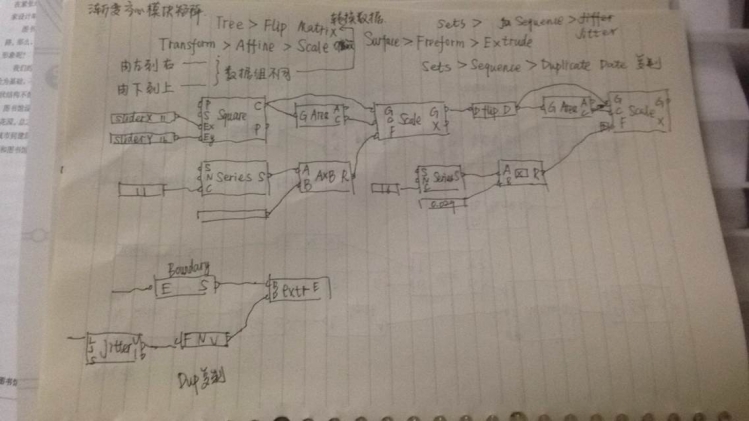
最后送各位还在Grasshopper中苦苦挣扎的各位同仁一句话，谦虚使人进步，沉下心来自己钻研，愿你们的树形结构之树越开越繁茂。

 

———————————————————————————————————————————————————————

本文所有内容版权均属于作者所有

欢迎您扫描下方二维码关注小黄人君的微信公众账号