今天我们来讲一下树形结构。前方高能，理论贴，请大家自备瓜子茶水，细细品味。

大家或许早有耳闻，Grasshopper最难的部分在于建模逻辑和树形结构。那么什么叫做树形结构呢？我们先来上一张神图：

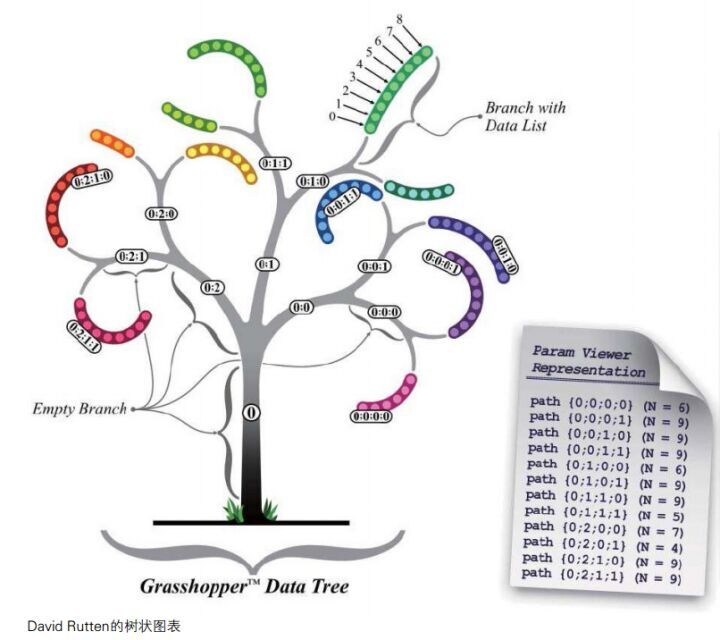
这是David Rutten前辈画的树形数据的图解。Grasshopper中的数据，粗略的讲，可以说统统都是树形数据，即使有些数据是线性数据，但是大家将他们接在Panel上看路径的时候，其实都是路径0下的。也就是说线性数据是树形数据的一种特殊形式，或者说大家都可以理解为树形数据。这里介绍一个运算器，Param Viewer，它的主要目的是用来观察数据的结构和路径情况。大家可以右键该运算器选择Draw Tree，来让其图像化显示数据结构。

图中的0,1,2这个运算器就是等差数列的意思，S端是开始的数字，N是公差，C是输出几个数。默认是输出从0到9十个数字。

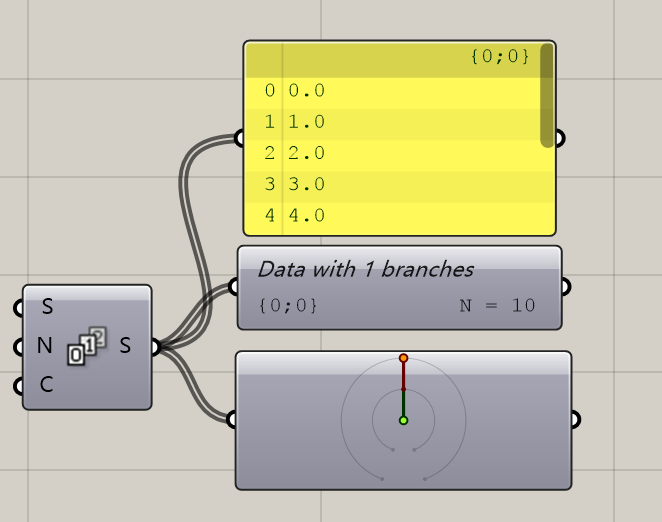
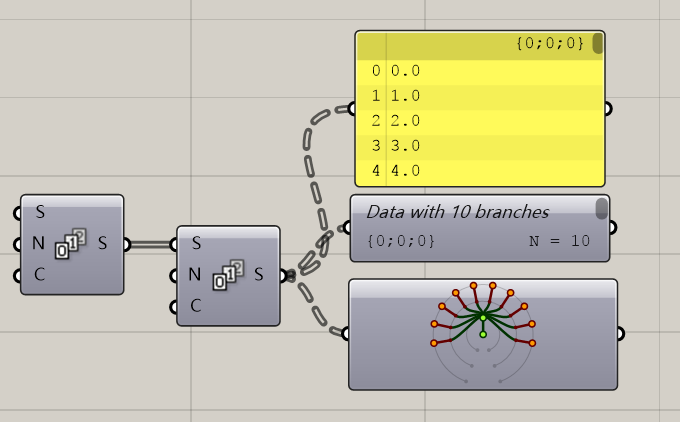
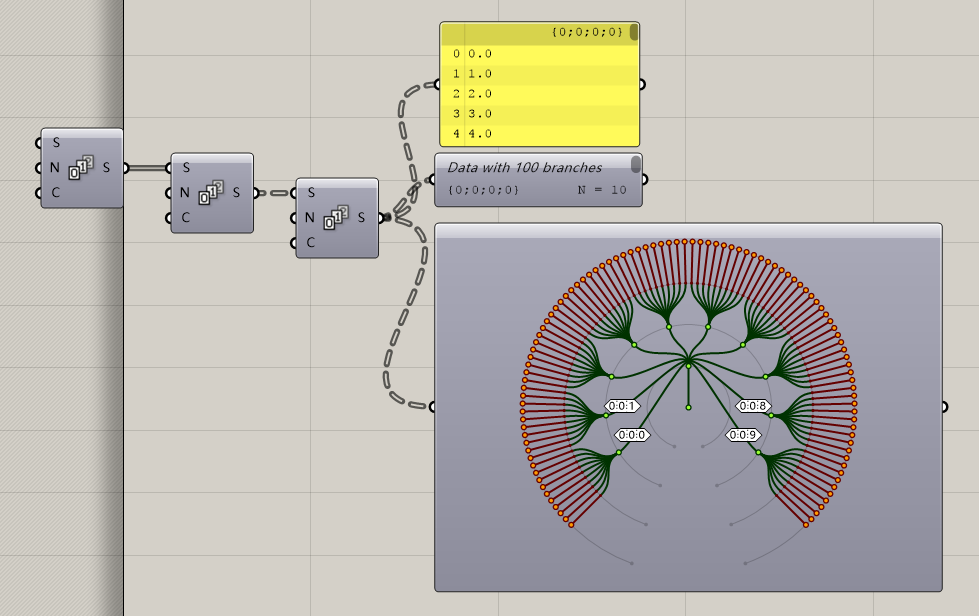
看了这些图可能大家已经蒙圈了，究竟什么是树形结构？下面我用我自己的语言为大家讲解一下。

正常我们所接触到的数学运算，比如上节课我们讲的3+5=8，这些都是在二维平面内的运算，大家相互都处在一个维度，可以互相发生关系进行加减乘除的运算。所谓的树形数据就是上升到了新的高度，三维空间里，比如3是处在A平面，5是处在B平面，即使他们都是数字，但是是没法相互加减运算的。换个更加夸张的例子，{0,0}路径下的数字3处在我们的宇宙中，而{0,1}路径下的5处在另外一个平行宇宙中，他们根本见不到面，因此没有办法互相进行运算。而这里的路径{0,1}，其中0叫做父级路径，表示的是他们都在0这个大宇宙中；而数字3是在0大宇宙中的0（子级路径）小星系中，数字5是在0大宇宙中的1号小星系中。

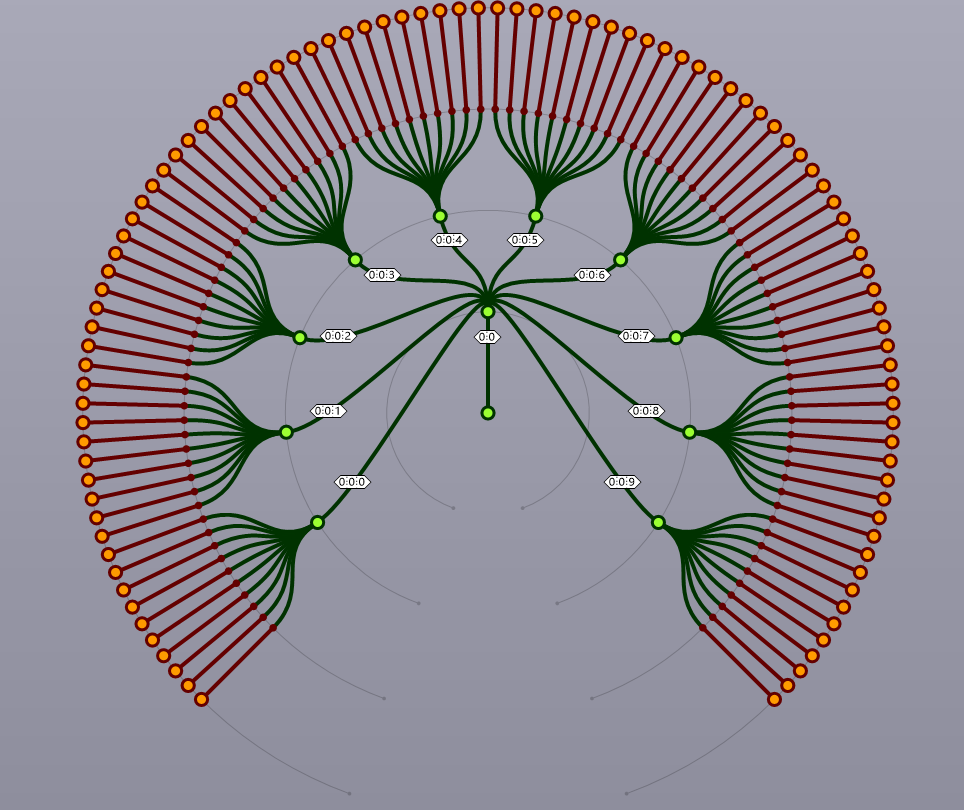
根据上边这个树状菊花图，我们可以很清晰的看出路径分级的概念。从最中间的绿点0出发，分出了一条主杆（树干）叫做（0,0），然后到了第二个节点，之后分出了10条分支，从{0,0,0}一直到（0,0,9），然后每一个节点又分成了10个数据，也就是（0,0,0）下的序号0-9十个序号，一直到{0,0,9}下的0-9十个序号。

事实上，这些所有数据的路径，除了第一位的父级0之外，后边都是在做0-9的变化。那么第一个0到底是有什么用呢？换句话说，从{0,0,0}{0,0,1}{0,9,0}{0,9,9}这样的变化中，我们完全可以把它简化为{0,0}{0,1}{9,0}{9,9}这样的路径名，少了一位，树状图也更加简化。我们用之前右键菜单的Simplify将最后一个等差数列的输出端给最简化路径处理，得到的新的数据结构如图：

大家可以看出来，最前边的父级0被删除了。那么这个逗比0存在的意义到底是什么呢？既然可以被删除，也就是没有用，那么为什么Grasshopper要强行给他加上一个0在最前边呢？而且是父级的地位，颇有傀儡皇帝之感。

其实这个0是非常重要的，试想，如果这时候又有一组数据和我们得到的这组数组进行相加，按照我们讲过的平行宇宙的概念，自然是在同一个维度空间的数据才能相互见面，发生关系，然后运算。如果我们得到了{0,0,0}到{9,9,9}这样一千个数据分支组成的数组B，那么和我们刚才用等差数列得到的数组A相加的时候，很显然只有B中的{0,0,0}到{0,9,9}才能和我们得到的数组A相加，因为他们都处于这相同的数组中。如果我们把{1,x,x}这样的一个分支拿来，Grasshopper会自动放在{0,9,9}分支后，不会融合在A中。因为他们的父级一个是0一个是1.换句话说，Grasshopper之所以为大家在{9,9}前加一个0，是为了防止后期运算的时候出现{1,x,x}这样的分支从而发生数据混乱。但是大家在很多情况的时候不会出现{0,x,x}和{1,x,x}两组数据运算的情况，很多时候数组A就是我们得到的最终结果了，这时候我将这个父级0成为“无效路径”，即：在我们已知用不到更高维度的分组进行运算的时候，最高维度0的路径就是无效的。为了简化路径更易于观察，我们可以Simplify掉这个0。如果你已经看蒙了，那么我们最后会引入三个案例作为泛读材料让你们更加感性的认识树形数据的运用。

 

树形数据是非常有用的知识，也是非常重要的知识，很多时候需要我们自己去悟。数据分组的道理其实非常容易理解，虽然我还没有见过任何一个人在任何教程中简单易懂的解释出来，所以我给大家解释一下吧：大家在渲染图或者画CAD的时候会分不同的图层，这样做的好处是，我们需要改玻璃材质，只要选择玻璃图层即可。Grasshopper也是这样的，当我们需要对某一分级数据进行处理的时候，我们直接选择其所在的层级即可。就是这么简单。但是由于树形数据比线性数据高一个维度，所以运算起来就会复杂很多了（大家脑补一下三维空间如果变成四维了，我们的生活会有多么翻天覆地的改变吧）。运算不但会出现数据匹配的知识，还会出现匹配方式（最长最短等）的情况。这些现在直接给大家讲解可能大家很难理解，因此我将这些讲解作为泛读材料（高要求水平）附在帖子里。大家如果有兴趣可以读一读。当然如果初级课程已经看完了还没有看完这些泛读材料，是达不到毕业的要求的哦！

 

我们简单的看一下运算时候会用到的几个运算器：

这三个是同组数据发生运算时候的联系。关于他们的使用，我会在泛读材料中讲解，同时我在Weave运算器的视频讲解中，提到了这三个运算器。大家可以看一下当“数字”变成“点”，加减乘除变成了连线（其实仍然是我们之前说的输入端输出端+操作手法的结构）后，他们的运算会有什么变化。

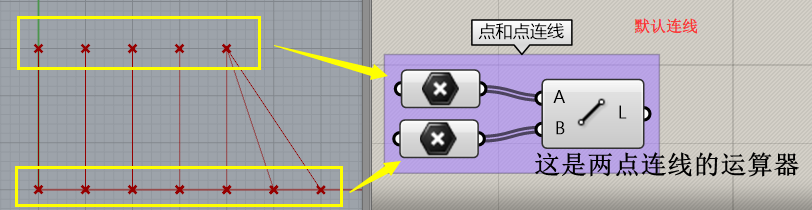
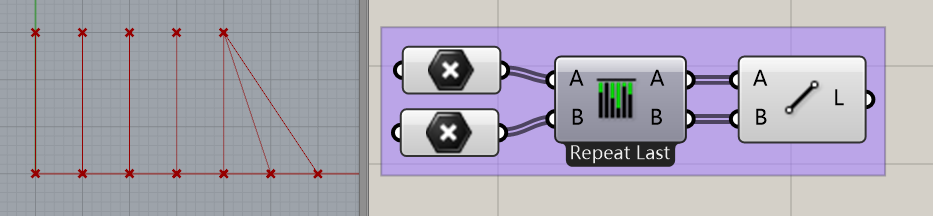
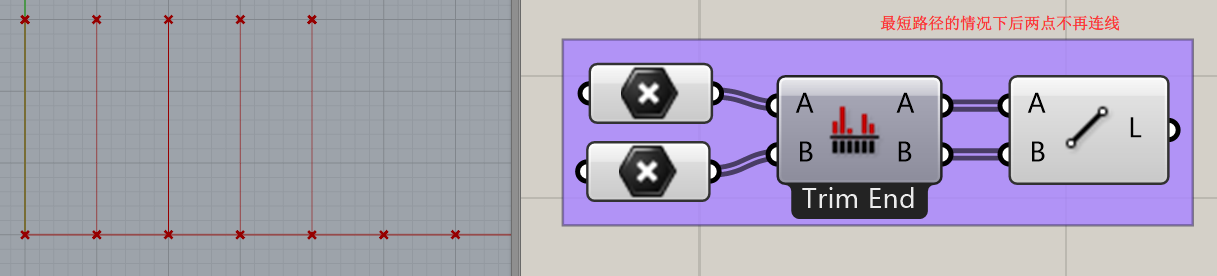
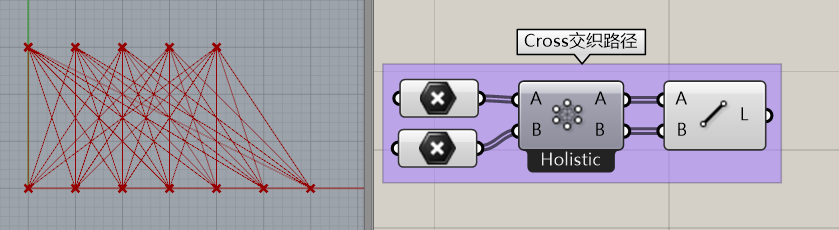
大家可以看到，当两个数据长度不同时，采用不同的数据运算关系会产生不同的结果。最长路径将会重复到最后一个点，最短路径一旦没有相连则不再运算。这有什么运用呢？打个比方如果你做了一个高层，两个不等高塔楼要做连廊…明白了吗？Cross交织就很好理解了，每个点都和另外一组的所有点进行运算。

事实上，这三个运算器曾经在老版本中是在右键菜单内的，现在被作为单独的运算器拿了出来，可见其重要性。

 

小技巧，在上边的案例中我们连入了两组点（分别在两个黄框以内）。如果是三组点怎么办呢？我们用滚轮放大这个运算器，会发现输入端输出端多了加减号。通过单击加减号我们可以为很多运算器增加输入端，以后我们会遇到越来越多可以增加输入端的运算器，比如合并Merge等。

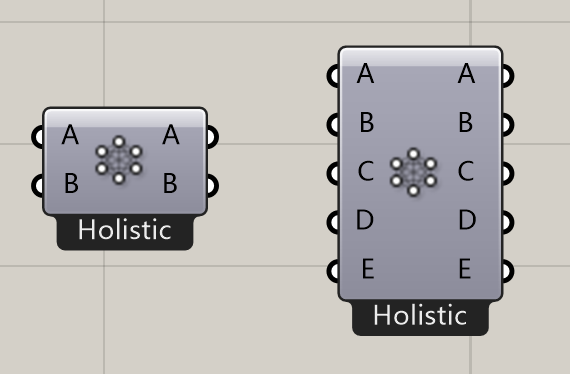
最后我们再讲一个对数据路径操作的小知识。很多时候我们需要将图层A的内容和图层B的内容进行合并，然后统一附材质，大家都清楚怎么做。如果我们在Grasshopper中想要进行类似的操作呢？我们怎么把{0,0,1}下边的数据全部移到{0,5,0,}中呢？这时候我们需要用到一个新的运算器，Path Mapper。

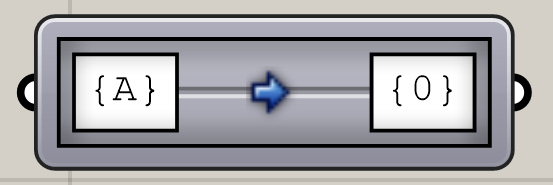
这个运算器允许我们修改输出的数据的路径信息。大家右键它，可以发现它提供了很多很多种修改方式：

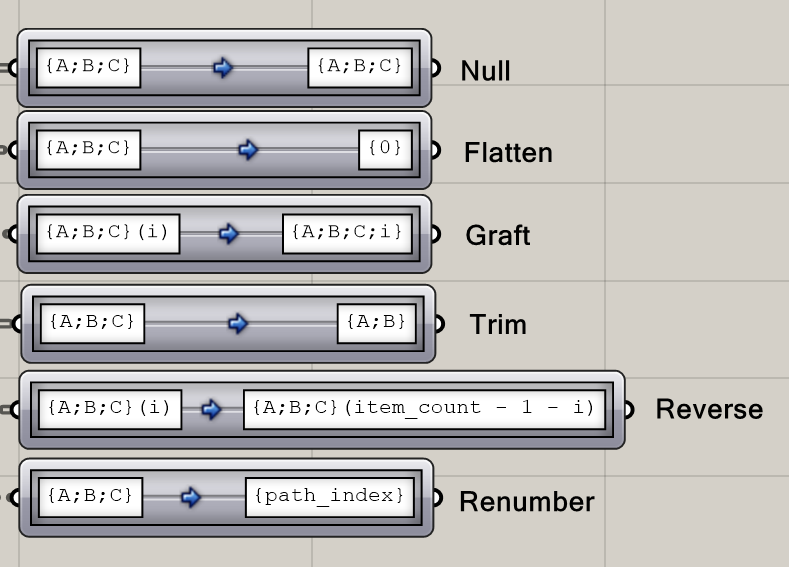
当然这些ABCi都可以进行修改，大家只要右键点Mapping Editor即可。大家可以按照实际所需对其进行编辑。

 

那么简单的树形结构的知识就讲到这里，大家消化吸收以后如果想要更深入的了解树形数据，可以阅读我所贴出的泛读材料。

 

泛读材料：

数据运算的讲解——Weave运算器，地址连接：

浅析Weave运算器

 

 

进修材料：

树形数据结合实例的讲解——两篇，选自我的《由浅入深学Grasshopper》系列教程，放在下一期以供大家从更加感性的角度加具体案例来了解这部分理论。感性加理性，希望大家可以对树形数据知识的理解更透彻。

数据类型的介绍：http://jinjieming.com/?p=176

深入了解树形数据：http://jinjieming.com/?p=185

 

那么今天的课程就进行到这里。布置作业：完成泛读材料的阅读和理解；完成Weave视频课程中留的思考题；完成两篇树形数据结合实例的讲解贴中的案例，并真正理解我为了感性讲解树形数据分组的概念所提出的“嫂子，丈母娘”比喻的含义，和“复姓”的含义。

 

下节课我将会根据群里学生的问题，来讲解关于数据结构中Graft和Flatten的含义，进一步加深大家对树形数据的理解。

 

爱你们的小黄人君

DanielJin

初级10-11

 

———————————————————————————————————————————————————————

本文所有内容版权均属于作者所有

欢迎您扫描下方二维码关注小黄人君的微信公众账号