今天我们讲解Surface后半部分实体类的运算器。首先我们接上一节课的“刺头”模型来讲解。首先为大家介绍一类“挤出”运算器,该类运算器的主要功能是让大家挤出物体所用。特征是运算器内含有Extrude单词。

第一个运算器就是最基础的Extrude,它不但可以用来挤出一条曲线,也可以挤出一个面,大家用挤出面应该会比较多。对照第二个运算器Extrude Along,大家会发现第一个运算器有一个“方向性”。那么这个方向性是根据输入端D来确定的。输入端D要求大家输入一个向量的方向。
在这里我们深入探讨一个问题,并且希望通过这个简单的探讨,来让大家学会如何在以后自己对运算器的运用范围进行深挖,通过换运算器进行横向对比。
当我们试图挤出一个实体的时候,这个运算器是无法正确运行的,即使它不会报错。
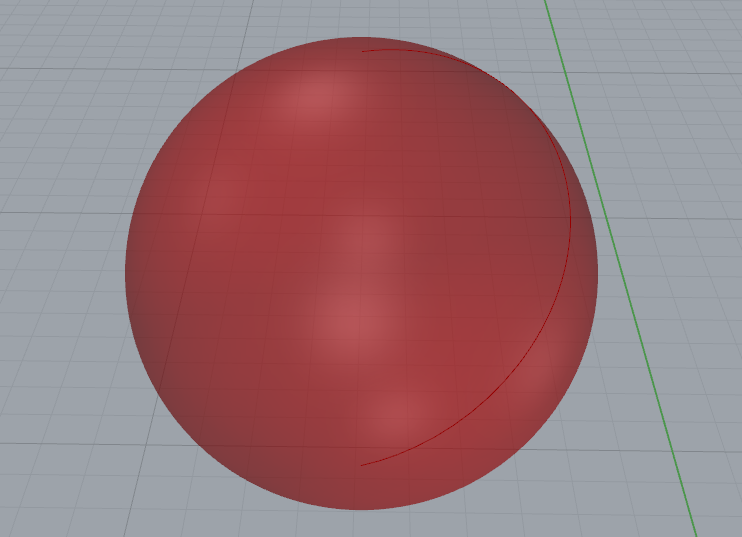
如图,当我们试图Extrude一个球体时,即使我们给了方向并且给了一个非常大的向量长度,球体还是原来的球体。我们把这个球体直接用Srf运算器进行拾取,发现依然无法挤出(改变条件进行对比)。这就说明并不是我们用了Brep运算器的问题,我们现在把球体的面切除一半,当这是一个空心球的时候,剩余的部分就只剩半个球壳了,这样就从Brep变成了Srf。

OK,这样我们的半个球面就一下一柱擎天了。
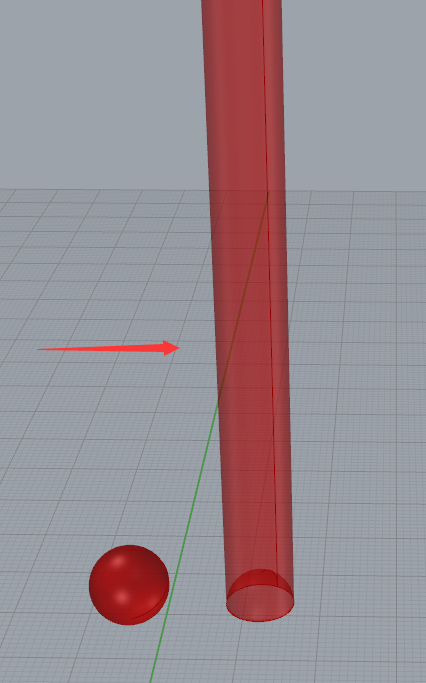
我知道很多人希望得到一个有“厚度”的球体,而不是仅仅是一层皮。这就相当于很多人SU建模的墙是有厚度的,他们会画一个矩形然后P拉起来高度。有的人建模则仅画一个外壳,墙是没有厚度的实体。如果我们想做有厚度的球体,那么应该用Offset这个运算器(该运算器有两个,一个是用于线的,一个是用于面的。)
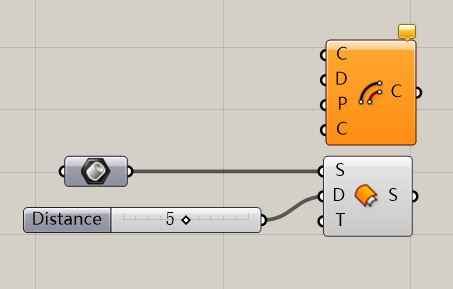
我们要非常,非常,非常认真的用“悬停大法”来观察这个运算器。同样对于输入端D来说,这个输入端是要你输入距离的,它并不是要求你输入一个带方向的距离(向量),仅仅输入一个距离值就好,运算器是自动按照法线的方向进行Offset的。有人认为这样我得到的结果(也就是输出端S)就是一个有厚度的实体球了。其实不然。我们利用悬停大法来观察输入端Brep和输出端S:
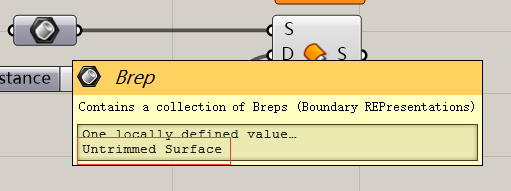
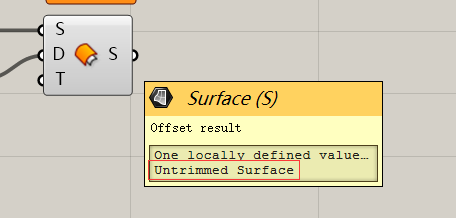
我们可以看到输入端和输出端的属性都是Srf。也就是说输出端仅仅是一个放大了以后的“面”。这是一个很头疼的问题,我们把它们Bake出来进行更好的示范。
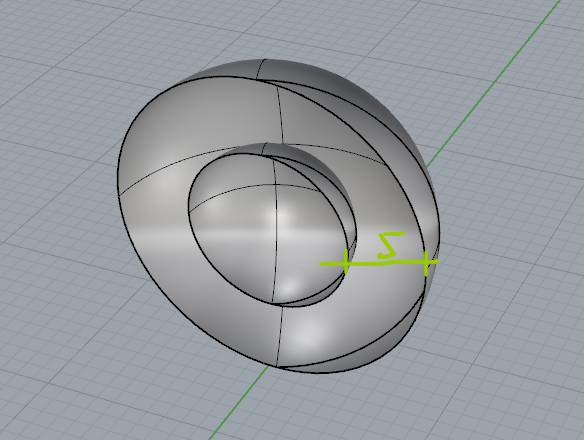
很显然,我们Bake输入端输出端后进行剖切,得到的是两个球面,并不是我们希望得到的实体。在Rhino中(甚至在SU中),所谓实体的建模定义并非是“实心的”(虽然实际上实体应该是实心的),电脑通常的建模方法是对其进行内外表面的建模然后中间是空心的(反正看不到嘛!)。因此大家要非常注意在剖面表达时对建模要进行一些后期补充(比如用CAD或PS加入剖面填充)——而这就是Revit最擅长的地方,他可以自动在导出施工图时自动进行后期补充。
回到我们刚才的话题,如果我想要得到一个实体怎么办呢?答案是,很遗憾,你无法从一个Srf直接得到一个实体。通常情况下,你需要首先进行offset,然后再把周边的面建立起来。具体情况可以看我的截图,总之是非常麻烦。(其中倒数第二个运算器是Sweep1,也就是Rhino中的单轨扫掠。和Rhino的双轨扫掠一样,我们GH中也有Sweep2,功能一样,不再赘述。)
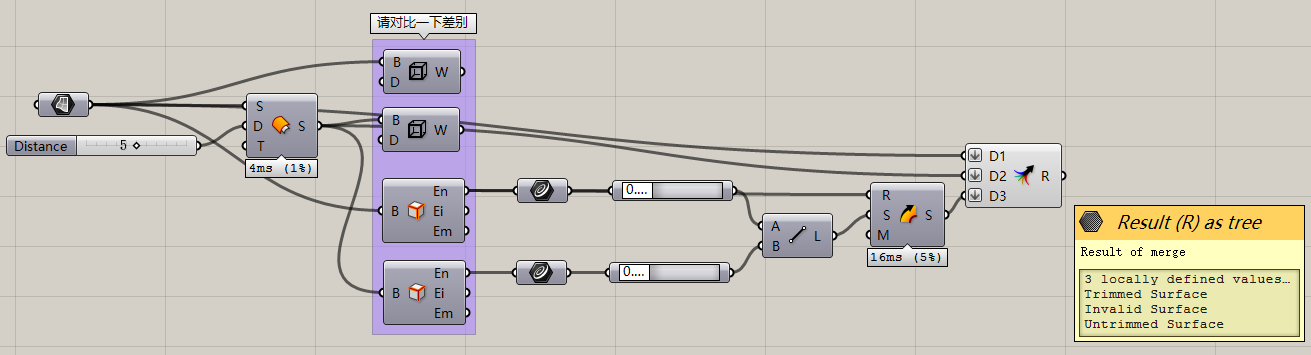
所以我这里推荐的是,Offset实体或者说由面生体的工作,请尽量交给Extrude。它可以生成非常令人满意的Closed Brep。
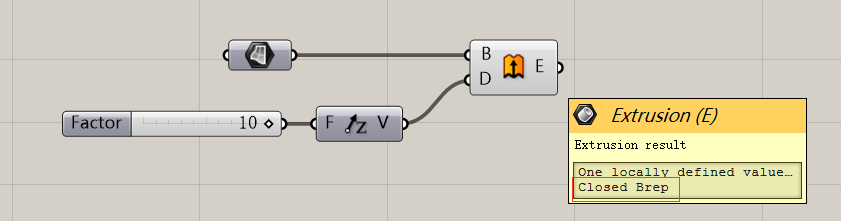
当然,我更加推荐的是,直接在Rhino中进行手工操作,同时选择上记录构建历史再用Grasshopper拾取。这样会增加你的联动性,你在Rhino中进行的操作,Grasshopper也会进行相应变化。
这里增加一个Grasshopper的运算器讲解:Geometry Pipeline

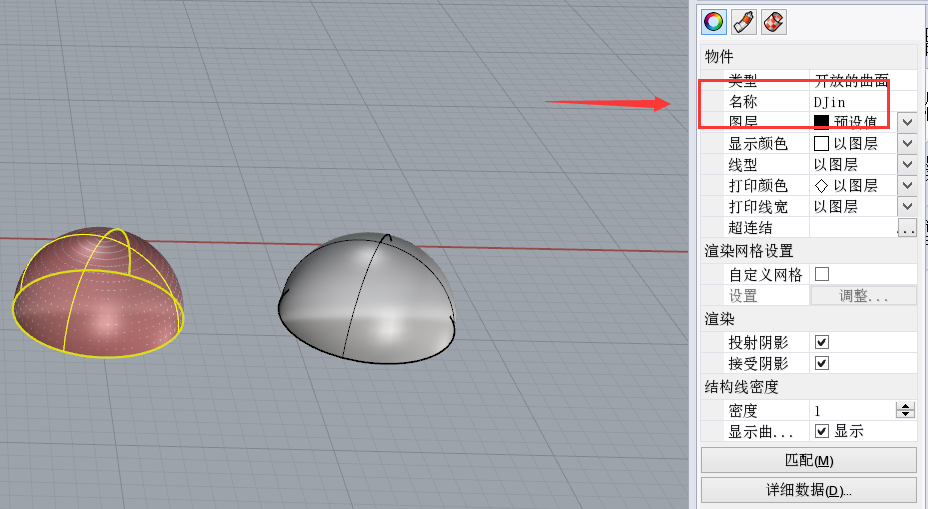
这是一个非常非常有用的运算器,可以直接读取你的Rhino中的模型。右键该运算器后,Layer部分可以输入你需要读取的图层的名称(*代表所有图层),Name部分代表你要读取的Rhino模型的名字。这里也许很多人都不知道其实Rhino的每一个模型的每一部分每一根线每一根面都可以取名字的!下边的Type表示你要读取的物体是点,线,Brep还是Mesh。如下图,当我给这两个半球面分别取名DJin和DJin2后,Pipeline自动拾取了左边的DJin半球面。无论我怎么对球面进行编辑,只要名字不变,Pipeline还是会拾取它。是不是非常方便?由于原Rhino文件我不进行上传,因此这个运算器请大家在Rhino中自己随手画点什么然后用gh附件去操作一下。
这就是一个“方向性——厚度问题”引发的思考。回到最开始,我们还有一个挤出至点的运算器没有讲解。这个运算器的作用实在太简单,我们把上节课的案例进行修改一下:

就得到这样的结果了。

接下来我们讲些新的运算器。
4Point Surface:从四个点创造一个面,非常基础的运算器但是却不常用。推荐大家面的生成还是从结构线生面,在Rhino中进行生面的任务。
Surface From Points:从一堆点中得到一个面。这个面是这些点的最适面。这里要着重说一下UV,UV是指这个面的结构线数量。当我们的结构线只有一条的时候,面就无法生成,同样当UV数值过大时,如果点的数量不够多也是无法生成我们所需的面(尤其是随手瞎点一些点的时候)。

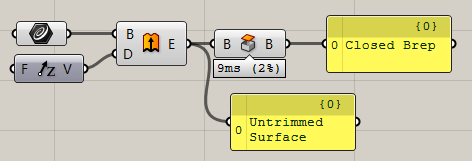
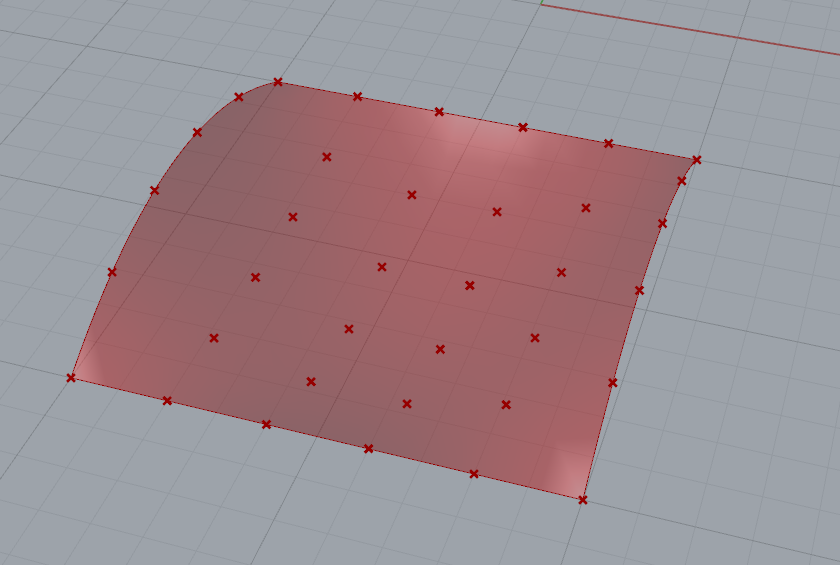
Boundry Surface:最常用的生成面的运算器,从围合的面的边界线生成面。但是在官方描述里没有说明的是,该运算器适用且仅适用于平面的面。当边线不位于一个平面内,则无法正确运算。
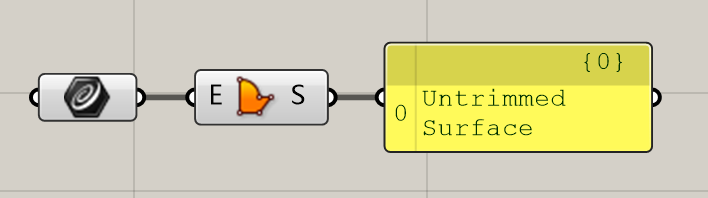
该运算器输出结果是宝贵的Untrimmed Srf,很多时候我们如果遇到了UV和Patch的麻烦,可以尝试用此运算器重新通过轮廓线生成Untrimmed面。
Loft以及Loft Option应该也是Grasshopper中比较常用的运算器了。在设置运算器中可以进行详细的设置。和Rhino中的Loft放样一样,唯一需要注意的是,很多时候由于树形数据结构复杂,所以大家要灵活使用。有时候与其调整结构调整半天,还不如直接放在Rhino中进行Loft。
同理,要灵活使用的和Rhino中功能一样的还有Pipe,Sweep1,2;也就是我们说的成管,单轨/双轨扫掠。
在生成实体类的运算器中,绝大多数都是给予简单输入端即可生成对应的Box或球体。非常简单而且和Rhino中的功能类似,按照大家目前的进度应该能做到拖出来看一眼就可以掌握。
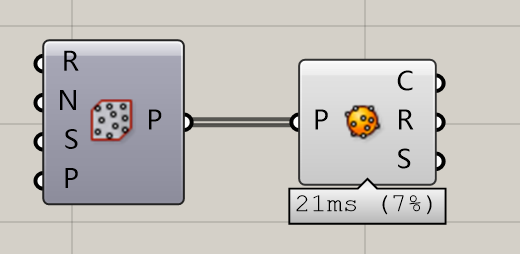
这里我们讲两个Rhino中没有的运算器,“按照适应性”生成最适球和包裹Box。
Sphere Fit会按照随机的点中,自动选择处于(或接近)某一个球表面最多的点,反向生成这一个球体。
而Bounding Box则会将输入端C中包含的物体用体积最小的Box包裹起来。右键可以选择是包裹每一个单独的物体(Per Object)还是包裹所有的物体(Union Box)。输出端的两个B则是根据坐标不同而进行的不同输出排序。
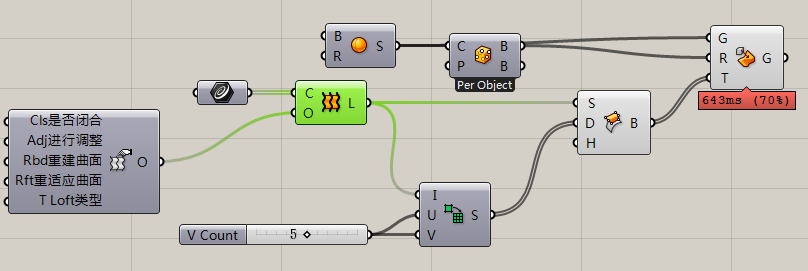

如图,这是非常简单的利用Box形变,对所包裹的球体采取同样形变然后铺满整个面的操作程序。这里面倒数第二个运算器叫做Srf Box,是通过一个Domain²来创建许多Srf上的Box。最后一个Box Morph运算器的作用是根据两个盒子的形变,将某输入端物体采用同样的形变处理。一个球生成了25个变形球,这是非常简单的数据处理问题。Box Morph通过比较原来包裹的盒子和现在这25个盒子,得到25个形变量Transform,将这25个形变量运用到原来的球体上得到你们看到的这个形状。
当然,也许很多人这时候会想到“流动”,我并不推荐大家把刚才这个程序成为“曲面流动”。严格意义上讲,曲面流动应该运用的是下边这个程序:
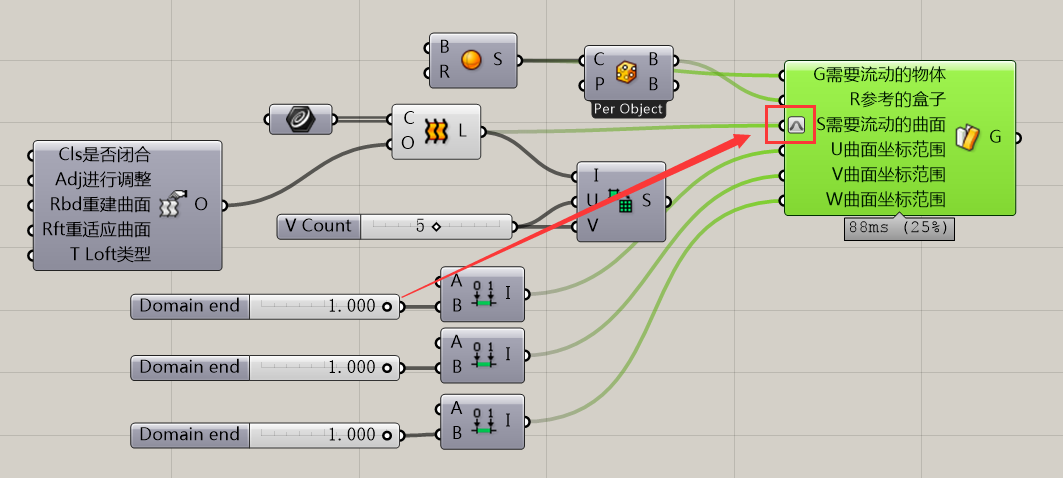
请切记将曲面重新自定义域,这样便于你们可以很快的控制流动范围。

看,一摊融化的冰淇淋/乌龟壳/体育馆的屋顶的草模很快就做出来了。
接下来的Isotrim和Offset我们都已经讲过了。我们把Surface中最后两个常用的运算器讲一下。首先是为物体加盖的Cap运算器。它可以给未封口的运算器进行加盖,生成Closed Brep。

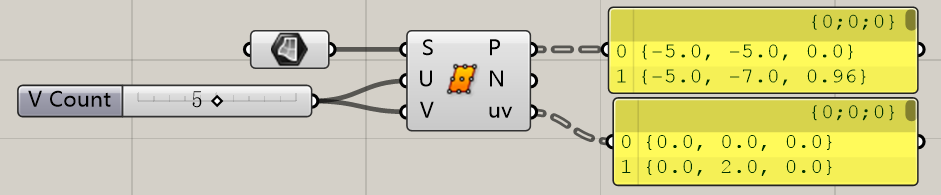
Divide Surface,根据给定的UV数目将一个Surface进行等分。其中给定的数目是U和V的Domain数,也就是说结构线数目要+1.我输入了5会得到6条uv线。并且输出这些uv的交点P,法线N和uv。不知道大家是否还记得我们讲过的“点和uv不相等”,这个例子大家可以非常明显的看到他们并不相等。尽管他们的“表现形式”都是你们所看到的这36个点。
最后我为大家讲解一个小实例,Copy Trim的用法。这是非常爽的一个运算器。它的用法通俗来讲就是根据一个面的trim情况,来trim另一个面。也许你听了这句话没有反应过来有多爽,那我换句话说。平面上你随手开几个洞trim一下就可以做到,如果是异形建筑就会非常麻烦。这时候你进行一下Copy Trim,一下就可以完成繁琐的手工任务。它的核心是对UV进行控制,在UV都为0-1的情况下(UV实际上是不同的,但是根据我们讲的重新自定义域和Remap映射,大家可以认为原参考面的UV直接映射我们的目标面UV)进行Copy Trim。因此这对曲面的UV连续性有一定的要求,大家可以看我的三分钟Grasshopper小讲堂——浅谈曲面连续性。
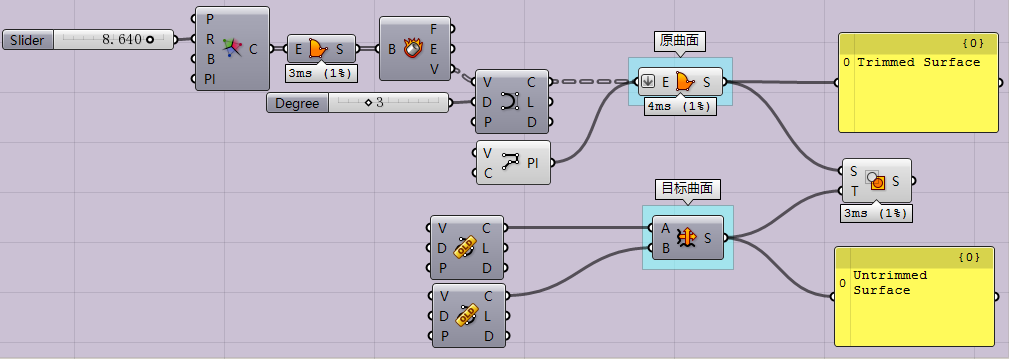

其中放样得到目标曲面的运算器叫做Sum Surface,它仅用两条曲线,用一条沿另一条就可以生成一个曲面。这个案例希望大家好好研究一下,特别是怎么做出来的Voronoi表皮。
祝大家进步大大!
爱你们的小黄人君
DanielJin
———————————————————————————————————————————————————————
本文所有内容版权均属于作者所有
欢迎您扫描下方二维码关注小黄人君的微信公众账号
