今天我们来讲解一下Surface类运算器,以下简称srf。我们知道Rhino中组成模型的三大元素是点线面,今天我们讲解的则是建模中最后一个元素面。
首先我们要讲解的最基础的运算器是Deconstruct Box。一看到Deconstruct,我们应该不再陌生了。它可以将我们的Box分解出平面及长宽高的Domain值。有了Domain值,我们可以在内部增加控制点(Attractors)来完成一些内部功能细分的任务。
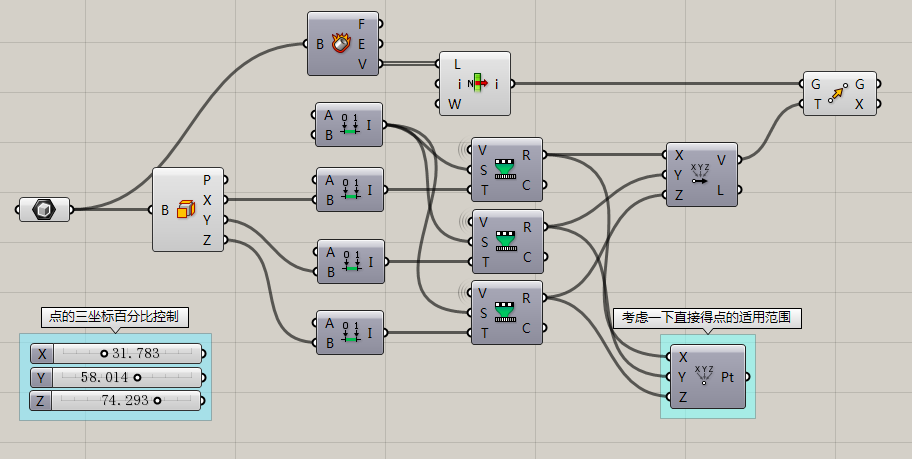
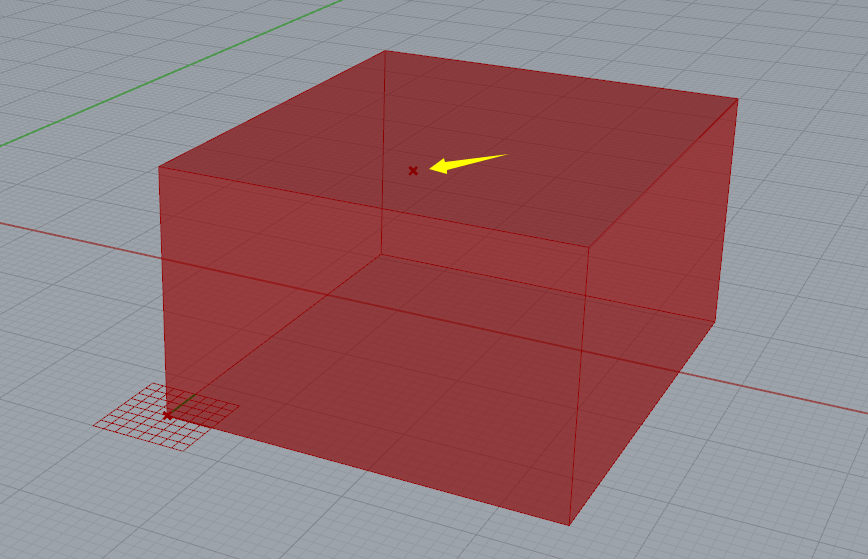
上图给的小程序是一个简单的在Box范围内生成一点的程序。其中要注意的有两点:
- 请大家思考一下,为何不能直接用3坐标得到点,而是需要先得到向量再得到点呢?(2)这是我今天在群里问的一个小思考题,很多时候我们在用拉棒调整一个变量的时候,设定了min max值,然后拖动一下得到了差不多符合比例符合审美的情况。在之后的调整中,经常因为我们修改了前边的某些自变量,使得这个拉棒的min max值不够用了,有时候我们需要扩大max值,有时候min-max区间太大又不方便鼠标拖拽调整。我们怎么得到一个min max值是前边某自变量的因变量的拉棒呢?换句话说,怎么能够尽量统一变量,让min max值根据前边的变量也进行自动变化?答案很简单,我们用拉棒控制百分比,用domain和remap来进行重新映射。这是之前讲过的运算器,看懂了吗?所以不要觉得教材看完了就学会了,知道运算器是干嘛的和学会用之间还有很大的距离呢!
接下来的运算器大多数是得到Box或面的外边界轮廓线,长度,Box框架的。这些是很简单的运算器,操作性并不大。大家知道有这么几个运算器即可。
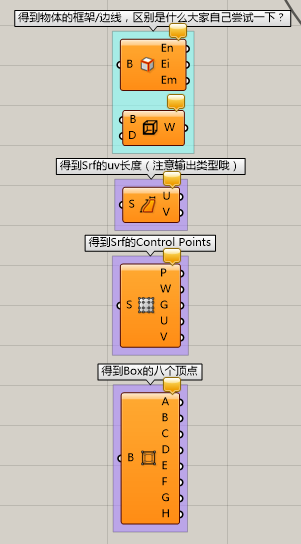
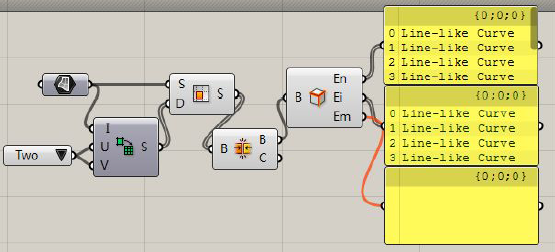
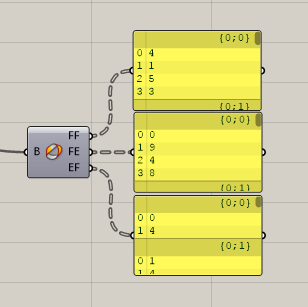
其中为大家翻译一下Brep Edges这个运算器,大家在简单Box中很少会将En裸露的边缘,Ei内部的边缘,Em非交叠边缘区别开来。
但是大家要注意哦,这个运算器可是不只是能使用在Box上,所有的Brep都可以使用。通过下边的插图,大家可以看出来输出端的内容是不一样的。
Brep Typology是用来获取并显示物件的拓扑属性的。这个运算器我到现在也没有在实例中看到过。如果我看到了我会为大家补充上实例。就目前来讲,大家想了解的话看一下完全学习手册便足够了。
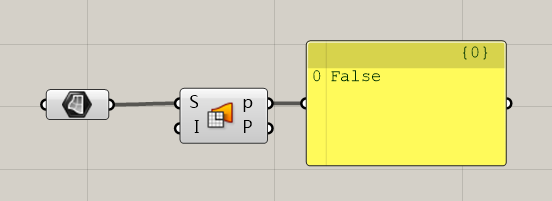
Is Planar是用来分析面是否为平面的,是目前0.9.0076新加的运算器。有举一反三能力的同学现在应该立刻意识到,既然有了布尔值,便可以通过输出True和False可以用Dispatch来筛选出需要的平面或曲面。接下来就可以达到平面开一种窗,曲面开另一种形式的窗子的效果了。
好啦,接下来终于到了我们的大主角——Deconstruct Brep了。这个运算器的威力实在太大了,大到我很早之前就讲解过了。这个运算器的主要作用是将一个Brep全部分解,得到它的顶点,边线和面。也就是说把一个Brep的组成三要素全部炸了,Boomshakalaka!但是首先大家要注意,既然是Brep,就意味着当你用一个闭合的曲线去炸开的时候,这个运算器会首先进行封面。
这个运算器有多么常用呢?可以说任何带实体的程序里,都有它的身影——尽管他的用法简单的不能再简单了。

同样常用的还有这一对兄弟。他们分别可以求出Srf(注意这里不仅仅是平面)的中心和面积,以及实体的体积和型心。很多人看老版本的GH教程中,有一个求圆心的运算器。很遗憾现在已经没有这个运算器了,类似logo的运算器变成了创建一个园。大家用这个运算器即可。

大家在之前的课程中还记得我们提到过的简单的干扰原理吗?就是得到最近的点,然后求出距离。这两个运算器可以得到距离实体最近的点和距离Srf最近的点。很多时候大家会把这个运算器和投影给搞混。其实很简单,当点能够投影在Srf或Brep上的时候,则是投影点;若超出了范围Domain²,则这个点会落在外轮廓线上。
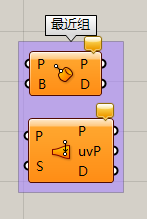
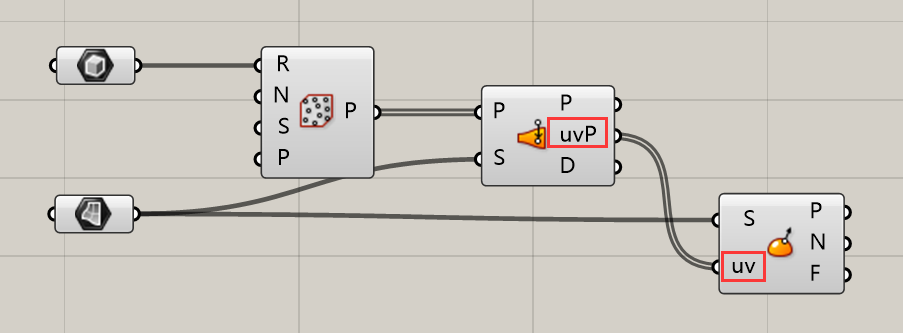
Evaluate Srf运算器主要是通过曲面上某一UV坐标值得到该UV交点的一些属性。比如该点,法线方向和平面。下边Closest和EvalSrf的连用是一个非常实用的小程序,大家可以很快的找到曲面上法线的方向。
在这里我想给大家普及一下uv的知识。大家或许已经非常清楚uv的概念了,就是曲面上的平面xy坐标系。这里我希望大家的认识能有一个质的提升,uv并不是一个点,尽管你们在脑海中总是会认为uv的交点它确实是一个点,这时候你们实际上已经“超越”了这个概念一步,进行了推理。本质上来讲,uv是一个二维数据(当然在uvw坐标系中则是w为0的三维数据),尽管他和点坐标在panel中的表达形式是一模一样,但是概念并不相同,一个是具象的点,一个是二维数据的坐标。
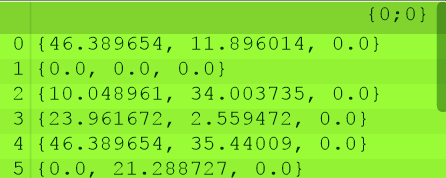
当uv值超出了曲面的范围的时候,这个运算器输出的结果会很诡异。
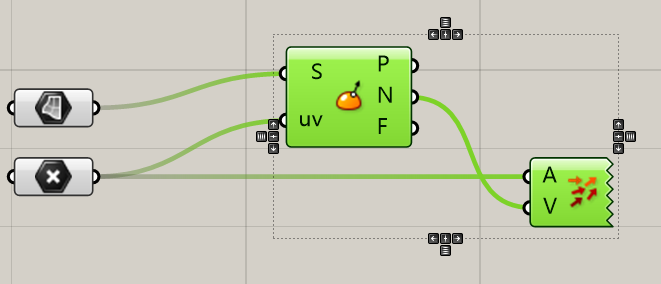
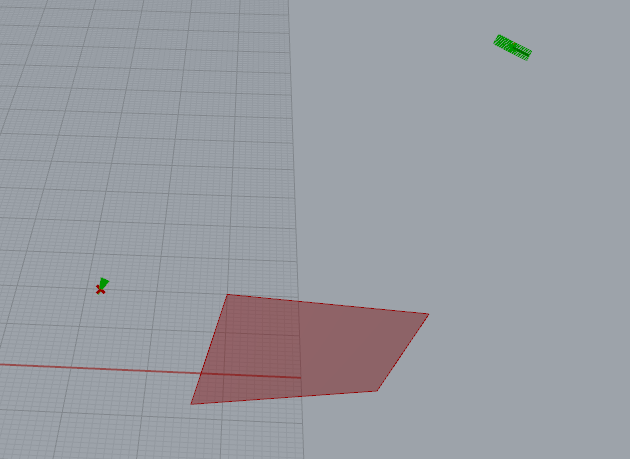
如上图,是不是很诡异?
刚才讲解了uv,根据最近群里的反馈,我觉得大家的举一反三的能力还稍弱,所以我给出一个小的Closest和EvalSrf联合的小实例。
这里面用到了一些非常常用的向量的运算器,而且向量部分可以有很多种方式,这里我只展现一种。
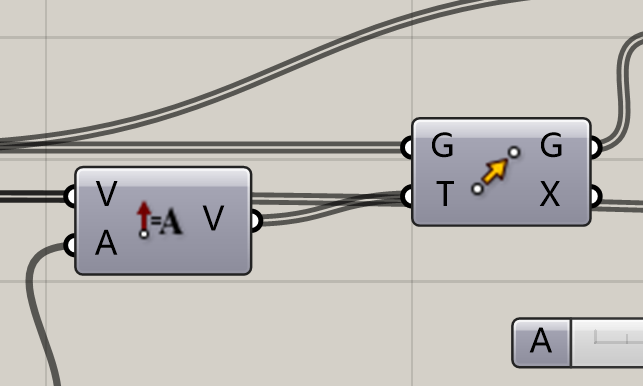
左边的运算器叫做Amplitude,他的作用是规定一个向量V和一个倍数A,得到长度为A倍的V向量。然后通过右边的Move运算器,对点进行远离球心向的偏移。经过连线后就可以得到下图的样子。

非常简单的原型,实际应用是大家能想到吧?

这个程序是这样的。其中有一点不同的是,我加入了逻辑判断部分。这个运算器叫做Point in Brep,主要是用来判断点是否在Brep内,然后根据位置关系输出True/False。有了布尔值,大家可以利用Dispatch筛选内部或外部的点。但是大家可以看出来加入布尔值以后,它占了系统很多资源。
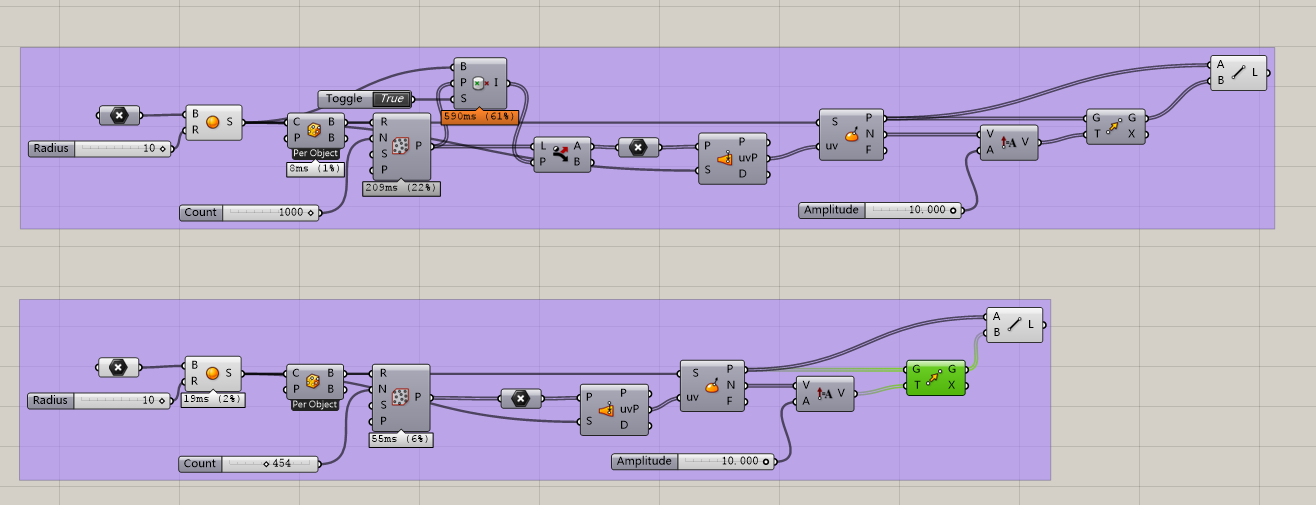
我们可以把这个原型继续深化下去,比如生成圆柱。

(不要用pipe,尝试读懂我的方法,更加节省内存。当然在现在的运算量下,loft更耗费内存,因为loft处理的是树形数据。但是当运算量更大的时候,loft会开始节省内存,理论上是这样的大家可以自行尝试一下。)
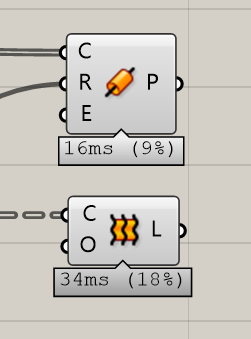

我们可以继续深化,利用我们已经学过的渐变,让圆柱离球越远,越细。
由于程序电池太多,所以截图已经看不到电池了,请大家下载附件查看吧。里面还有很多知识点,比如映射和乘法,我都放在电池的备注中了。模型的结果是这样的:
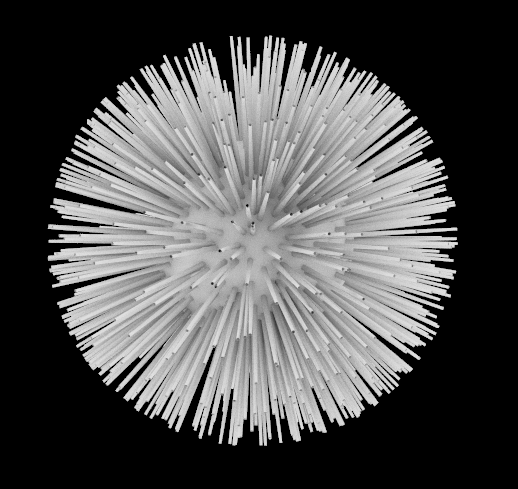
当然也可以做成这么一个小东西

我们甚至可以加上颜色和渐变,让整个球体五颜六色,也可以在远端开花,只要筛选出最远端的圆,得到圆心然后做一个开叉即可。随着大家学会的运算器越来越多,可以叠加的效果也就越来越多,程序也会越来越复杂,但是归根结底,都是由简单的一块块模块化所组成,这也是后期的高级课程中最基本的思想。因此我不断强调“举一反三”的能力,就是希望大家能够通过基础运算器的学习,进行锦上添花的操作。
希望大家可以把这个实例看明白以后自己做一遍。明天我们继续讲解Srf创建实体的运算器。
爱你们的小黄人君
DanielJin
———————————————————————————————————————————————————————
本文所有内容版权均属于作者所有
欢迎您扫描下方二维码关注小黄人君的微信公众账号
