大家好，好久没有发文。今天为大家发一篇关于Mesh流动的内容。

 

我们都知道“曲面流动”是Grasshopper中一个重要的知识点。让我们先来复习一下曲面流动的大致思路。曲面流动的主要内容就是将需要流动的单元用一个Bounding Box进行包裹，然后将流动目标曲面进行细分，在表面根据曲面的uv划分出一个个小Box，然后将流动单元一一“移动”到曲面上的小方格子中。相关方法有很多，我们展示一种：

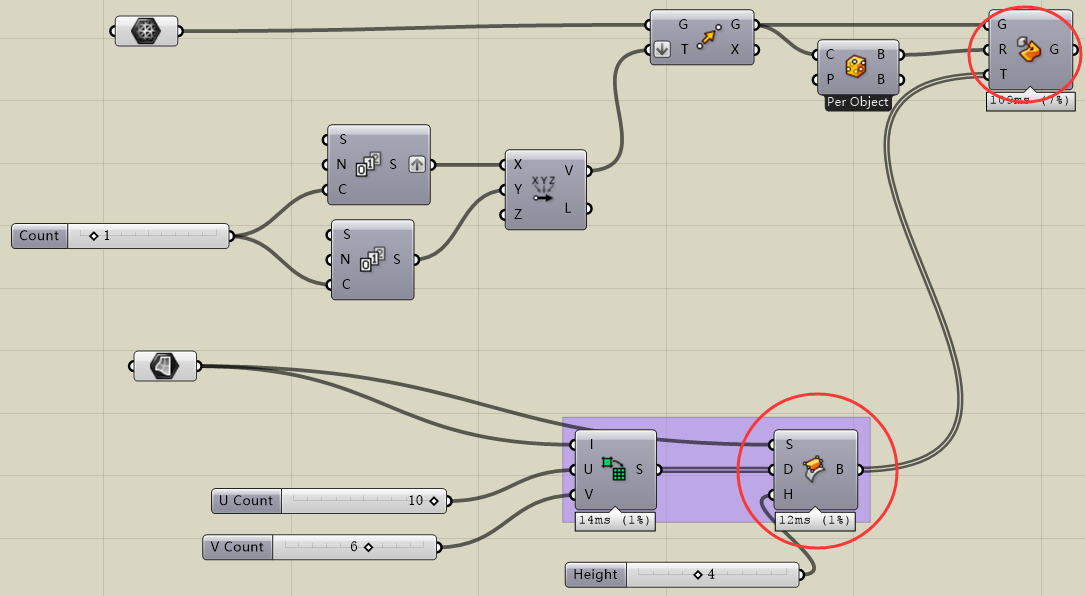
红圈内电池为重点电池

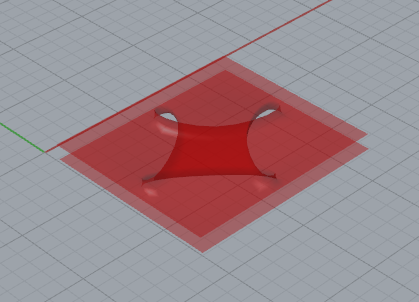
待移动单元

 目标曲面，将其表面按照UV划分后生成一个个的Domain Box

将移动单元用Bounding Box进行包裹，然后将其与目标曲面上的Box一一对应，从而将目标单元移动到曲面上。

 

 

如果我们流动的目标曲面不是一个Nurbs曲面，而是一个Mesh面，这可就难为到许多人了。因为我们并没有UV可言。但其实只要你学会了相关的道理，运用起来并不难。

我们先来看一下完整的程序截图：

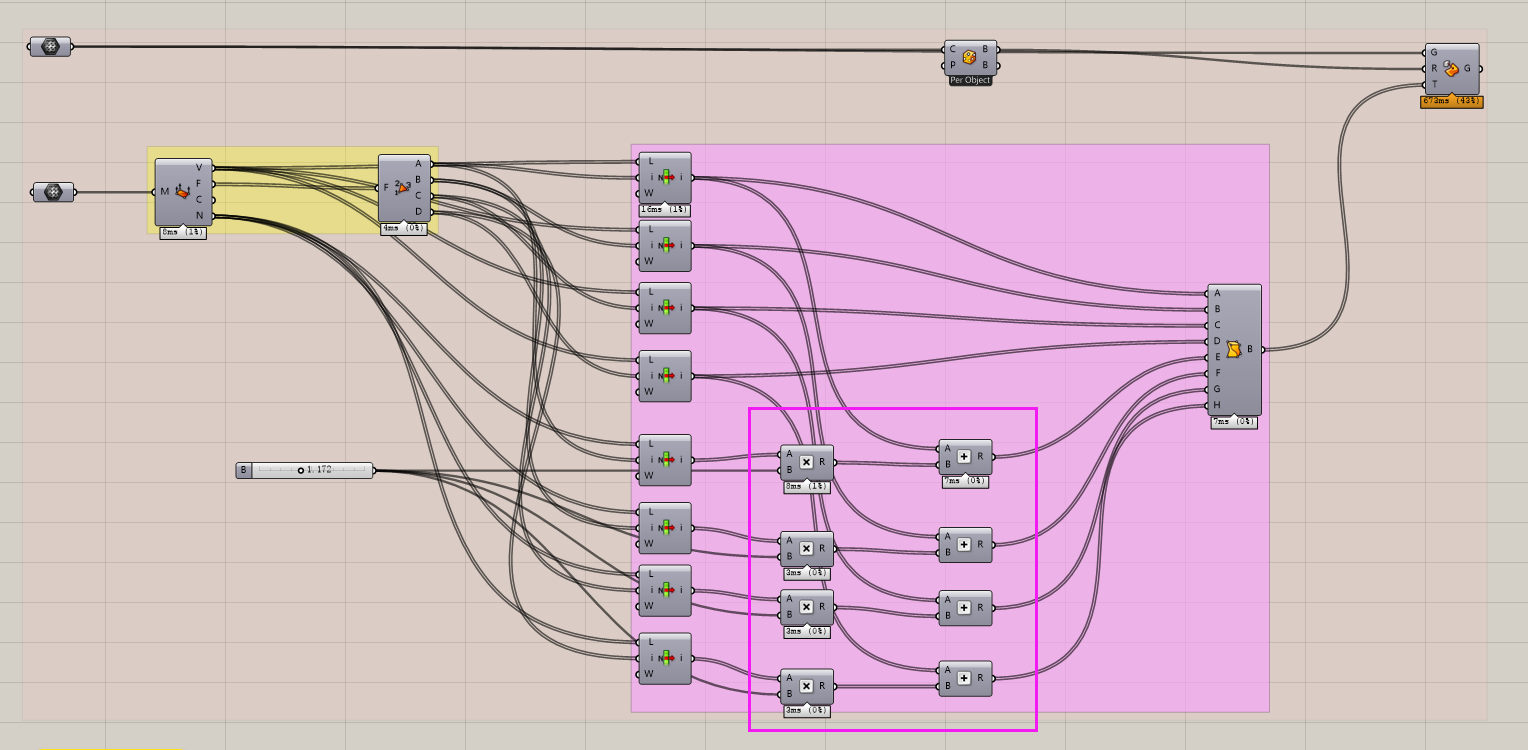
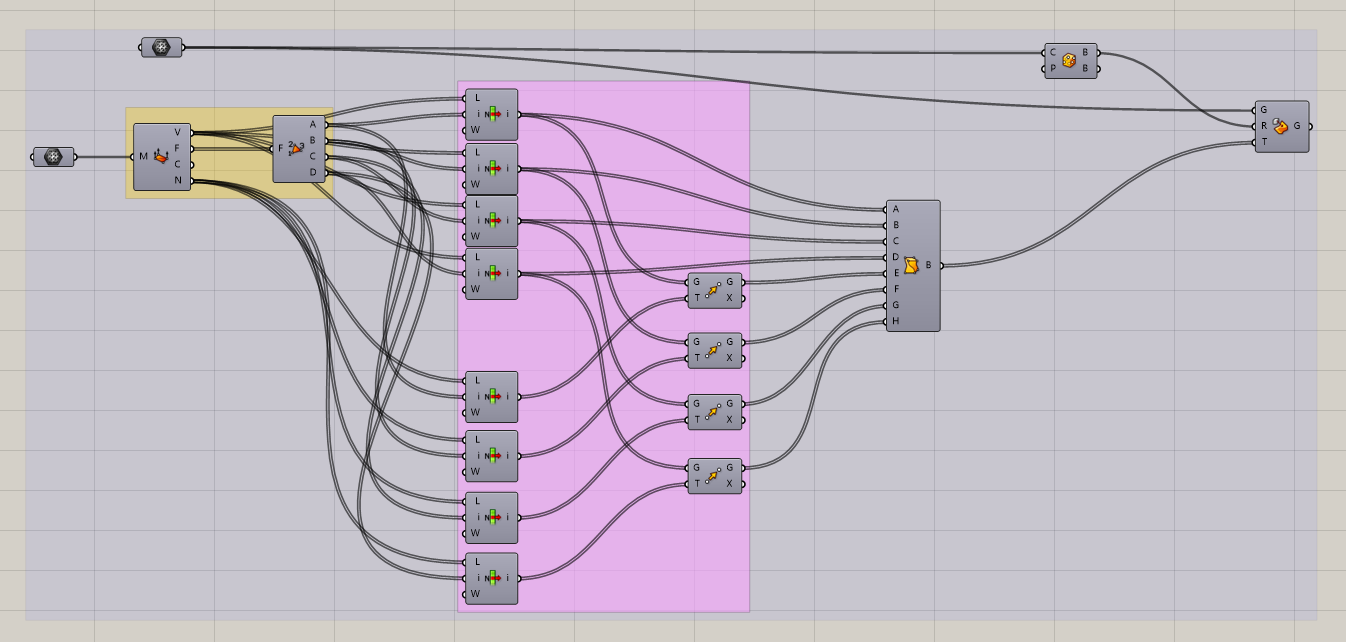
这两种方法完全一样。唯一的区别是下图直接运用了Mesh的法线向量，而上图中增加了变量，因此可以控制流动层的厚度。

 

首先我们需要知道，Mesh在Grasshopper中的定义有四个元素：顶点V，顶点组成Mesh面的顺序F（对于一个Mesh面来说，顶点顺序1-2-3-4和1-4-3-2是不同滴！），面的法线方向N（其实这个由F即可决定。比如上边给的例子，如果1-2-3-4的顺序是逆时针，还记得初中物理课学过的右手定则吗？四指逆时针并拢则拇指朝上，法线则向上；若1-4-3-2则四指顺时针并拢，拇指朝下，法线向下）。对于最后一个元素颜色C，这是Grasshopper里的特质。在Grasshopper原生的电池里，一般情况下颜色是不可以被Bake出来的，只有Mesh这种自带背景音乐颜色的逆天属性可以直接Bake出颜色。因此我们可以认为，对于常用的范围来说，Mesh最重要的就是V和F两个属性。

 

根据曲面移动的逻辑，我们也可以做出类似的流动。首先我们需要把一个“由多个Mesh面组成的Mesh体”炸开（Deconstruct Mesh）成许多小的Mesh面。因为后期我们要生成Box，所以这里建议大家还是用四边Mesh面吧（Mesh实际上只有三角面（T型，即Triangle型）一种形式。Grasshopper中有四边形（Q型）Mesh面，实际上还是两个T型面的组合）。有了小小的四边形Mesh面，这一步对应之前的曲面流动其实就是把整个Nurbs曲面按照面域的定义进行了划分（Divide Domain²）。

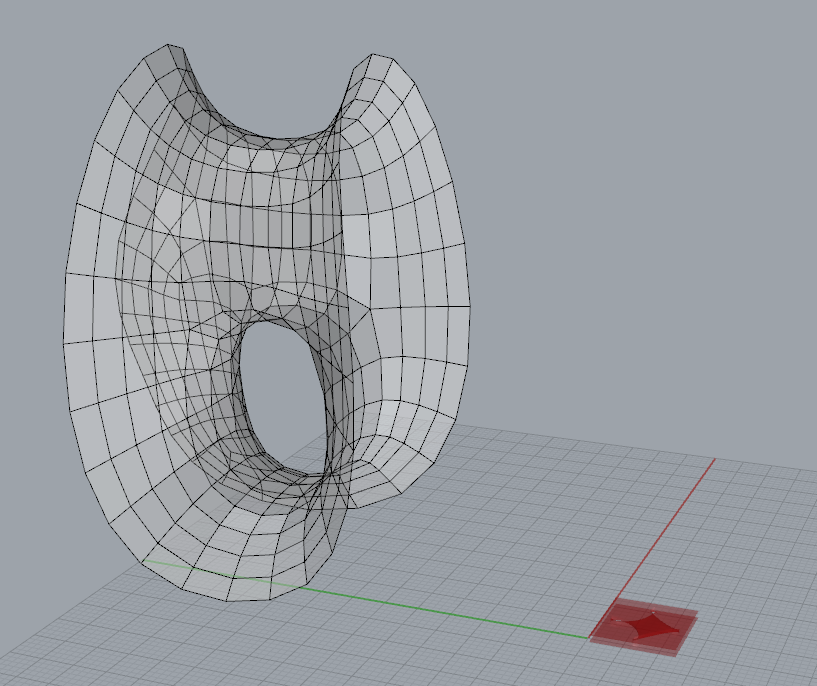
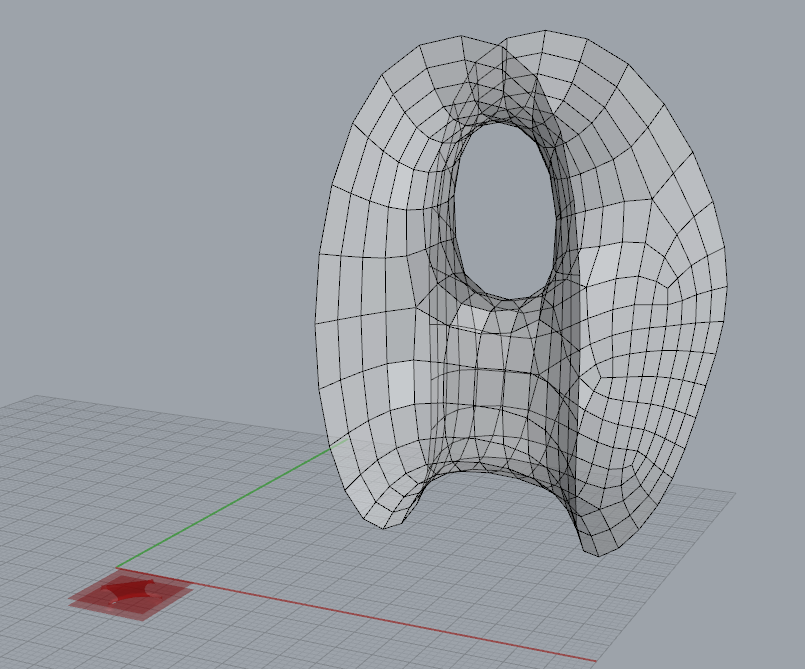
上图为待流动的单元和要流动的目标Mesh面。该案例中以一个四边Mesh面组成的“最小曲面”为例进行演示。

 

接下来的思路则是生成Box。在Rhino或者SU中如果你有了一个四边形的面，你该怎么生成一个Box呢？直接Pull/Extrude出来即可。由于我们有了法线向量，所以直接用这个Mesh面的四个顶点按照法线方向移动一定距离即可生成Box的另外四个顶点。

下一步我称之为整个程序的精髓：Twisted Box。用一个本来应该制造“扭曲的Box”的电池创造一个不扭曲的Box，相当于我们曲面流动中创造Domain Box。

 

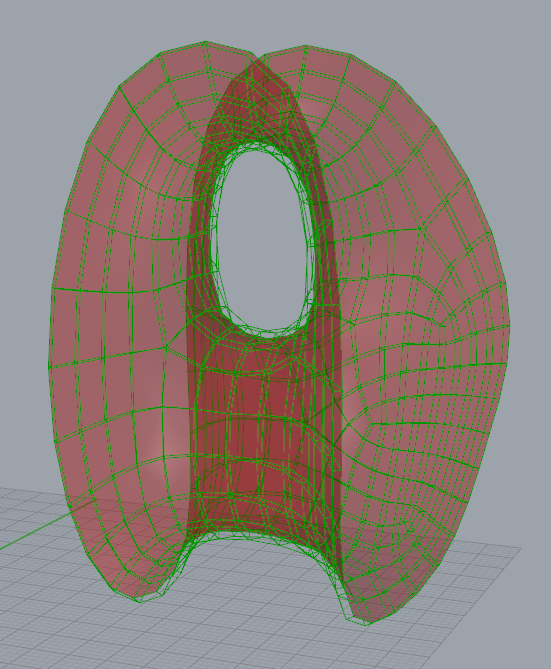
这样我们的移动目标Box也生成了，最后就是让这些Box一一对应然后将流动单元一一移动进去即可。

 

案例文件下载：

Mesh Morph