今天我们来学习的是Grasshopper中的“范围”的概念。我在泛读材料中提到过一句话——参数化设计，离开了参数便什么也不是了。那么说到参数，大家能想到多少和参数有关的概念呢？自变量，数据类型（整数小数，数字或字符甚至曲线曲面，线性或树形），数据取值的范围，若干变量的联动性……似乎大家能大致理解这些含义，却又无法用语言表达具体内容，只能有一种感觉。如果你已经到了我说的这种状态了，那么说明你已经开始入门Grasshopper了。继续认真努力地学习下去，你悟到的内容会越来越多。

关于“范围”，我们从最开始的拉棒运算器就接触了这个概念。拉棒的最大值减去最小值就是拉棒所表示的自变量的范围。今天我们来讲一些表示范围的运算器。关于范围的运算器有很多，我们在初级篇着重讲常用的，其余不常用的我们只简单讲述运算器基本属性，大家根据之前我们讲过的悬停菜单看输入数据类型可以举一反三，大致了解作用即可。

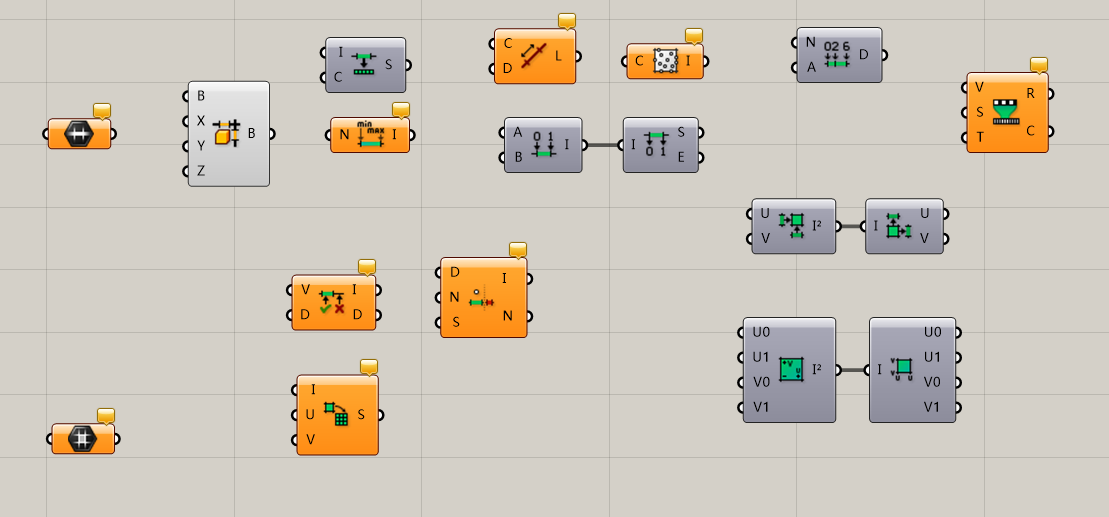
种类繁多的Domain相关运算器。

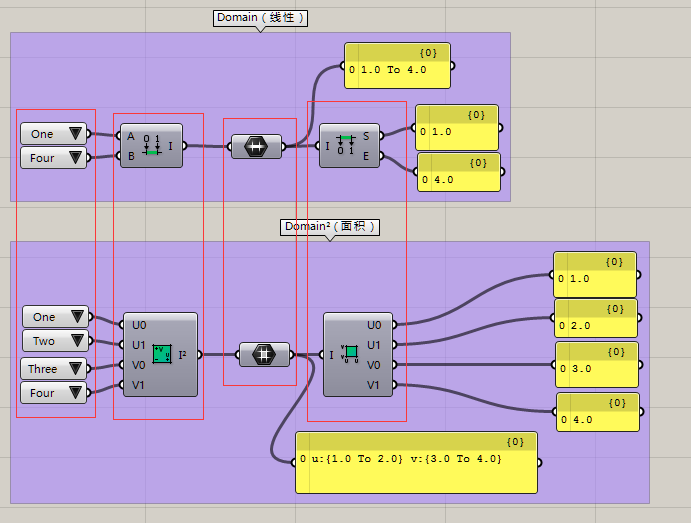
Domain类运算器可以分为两大类，分线性Domain和具有面积属性的Domain²。通过上边这张截图大家应该可以看出每个运算器的作用。我们在第一个红框设置了数值输入运算器，第二个红框内的运算器作用都是根据输入数值创建Domain/Domain²。第三个红框内的是在Params标签下，我们之前讲到过“主要作用是拾取物体，联系物体的桥梁”的“身份名片”类运算器，第四个红框则是分解该Domain得到它的临界值。

uv坐标系的意义和自定义域reparameterize
讲到这里大家可能发现了，在线性Domain中我们的临界值是字母A和B所表示。那么在Domain²中，我们用的是U和V。这个U值和V值我们在最开始讲Nurbs建模中提到过，在这里我们需要重新细致讲解一遍。
在我们所熟知的坐标系中，常见的用来表示位置的坐标是xyz，我们称之为平面直角坐标系-xy coordinate。那么由于我们在Rhino中经常要建立曲面，而曲面很显然是不能用xy坐标系所表示的——曲面应该是连续的，如果用xy或xyz表示，大家设想一下我们怎么表示呢？用无限个点的xyz坐标来表示？繁杂且不连续。所以我们需要用函数曲线来表达这个曲面，规定这个曲面的两个方向，比如x和y方向，所有x方向的线我们可以列无数个函数方程。同时这个方程需要是渐变的（因为是曲面，会有起伏），那么为了保证这一条条线之间没有“间隙”也就是足够连续，我们还需要在y方向上列出无数个函数方程，他们叠加得到我们的曲面方程。依旧很麻烦，但是这样的思维推进过程使我们得到了uv坐标系——结构线u和v互相垂直，曲面上任意一点都可以用u的值和v的值来表示。这时候大家来看Domain²的截图，很显然这是一个范围U：1~2，V：3~4的范围。它的面积是1.
我们在运算中，常常发现u和v值并不是整数，他们可能是一个无限不循环小数（这是很常见的）。而且对于我们实际使用来说，经常需要进行的操作是找到这个Domain²中的点或线，而不在乎它的总面积是多少。于是伟大的科学家们引入了一个“相对坐标系”的概念。我们不再关心这个点在这个uv范围内的绝对值坐标，而是只关心这个点所占的百分比。如果说这个点所在的范围分别是U：A~B；V：C~D，那么在相对坐标系中，这个点的坐标就从（u,v）变成了[(u-A)/(B-A),(v-C)/(D-C)]。比如我们知道了点N的相对坐标是（0.5,0.5）那么我很容易判断这个点在U结构线的中间那条，V结构线的中间那条。这就是我们在之前讲的“重新自定义域reparameterize”的由来。它可以大大简化我们的表达和运算，也更加方便我们去控制变量来生成点——我们不必再求这个范围的u和v最大值——如果我们输入的u和v大于最大值或小于最小值，点就会跑出这个范围了；我们只需要输入0~1的参数即可。

我们再来看看其余了解即可的运算器的用法。

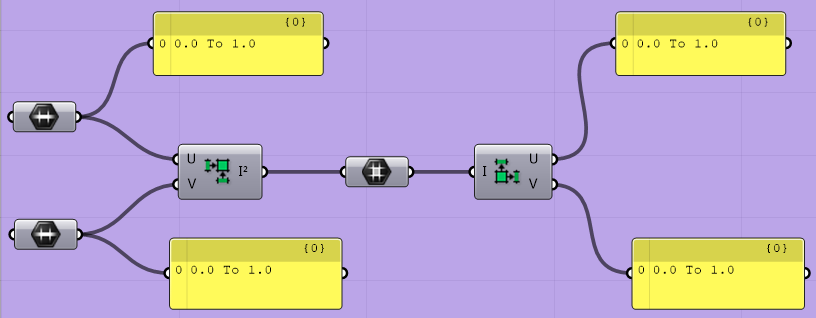
这个运算器和之前的建立Domain²类似，它们甚至名字都一样。只不过这个是用线性Domain范围来创建，而刚才我们讲的是需要用两个临界值来创建。由此可见Grasshopper是非常人性化的，它提供了很多创建方式，当我们输入端是一个Domain的时候就不需要拆分成最大值最小值再创建Domain²了。

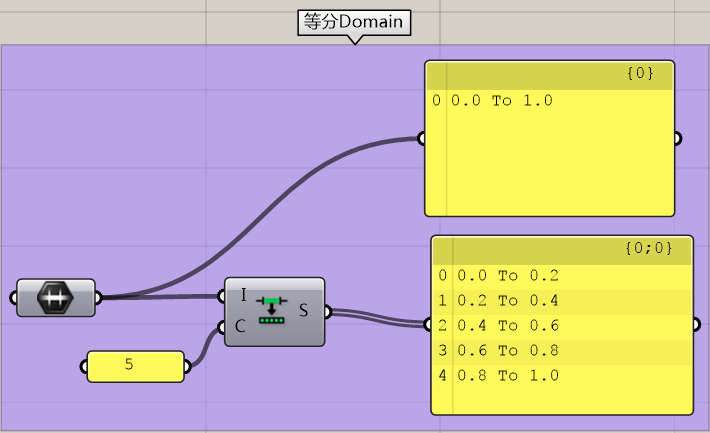
这个运算器很简单，等分Domain。

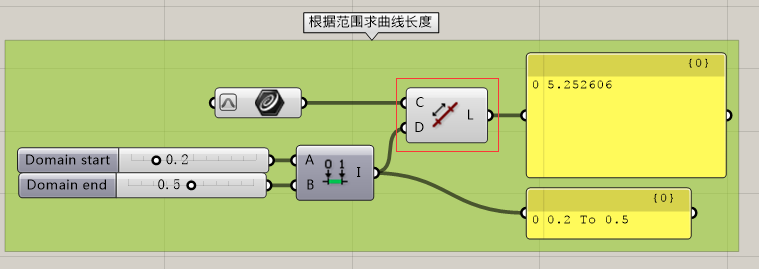
这个运算器是根据范围求曲线长度。注意，这里我对曲线进行了reparameterize处理。

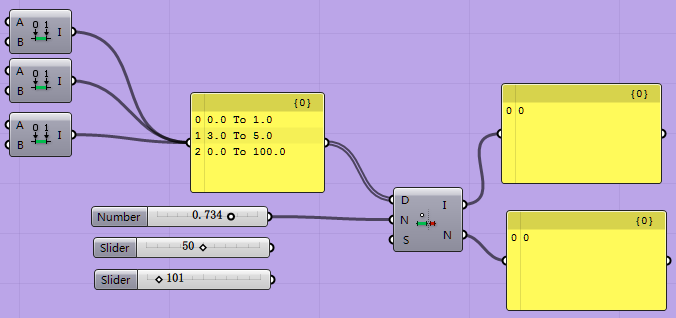
该运算器是求输入端N所输入数字是否在D输入端输入的Domain内。如果不在，I端输出-1，同时在N端输出该数字离哪一个Domain近，并输出它的序号。如果在，会输出这个范围在D中的序号。案例文件中我配了三个拉棒，请大家分别连入N，观看一下结果，应该就能明白了。

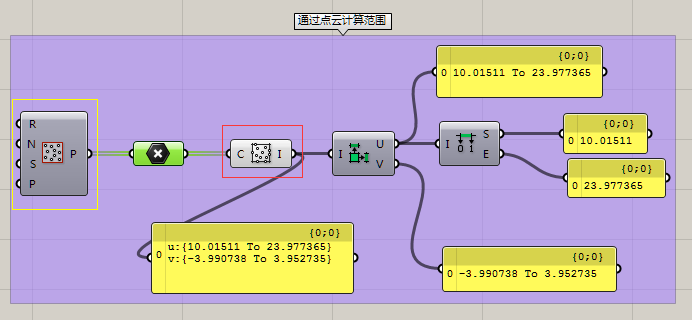
在这个截图中，黄色方框内的运算器是用来在同一平面内随机生成许多随机点的。红色方框内的运算器是根据这些点云，来计算u和v方向各自的临界值。这是一个比较有用的运算器，我们可以根据很多控制点（Attractor Point）——我们可以赋予它们一定的含义，比如说走路的人群，车子等——来计算交通压力，活动空间需要的范围。这些我们会在后边提高篇的案例中进行讲解。

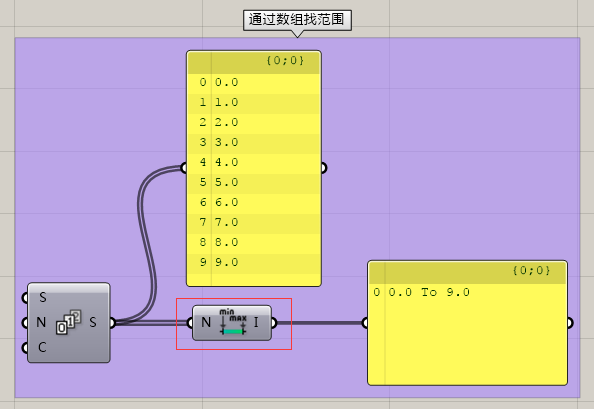
这个运算器是很有用的，它和上边的类似，是通过分析数组中一大堆数字，找出最大值最小值，然后建立起Domain。

我们接下来介绍三个非常重要的Domain运算器。
首先Consecutive Domains，这个运算器是根据一系列输入的数字产生一系列Domain。要注意的是，根据布尔的不同，其产生结果也不一样。False情况很好理解，就是第一个数到第二个数，第二个到第三个……True的情况则是第N个数的累加到第N+1个数的累加作为Domain的临界值。

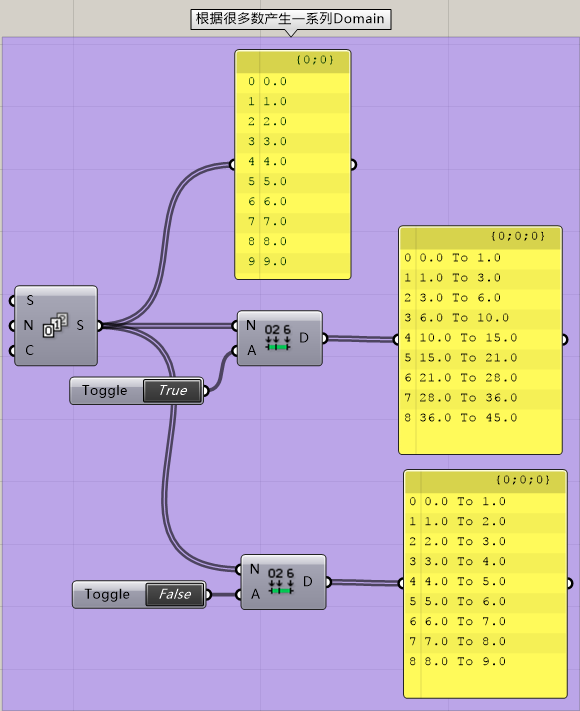
大家还记得我在E拓参数化论坛布置的一道参考题吗？求如何用等差数列Series运算器做出这样一个数列：

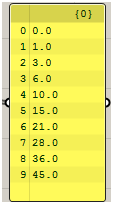
当时公布的正确答案是：

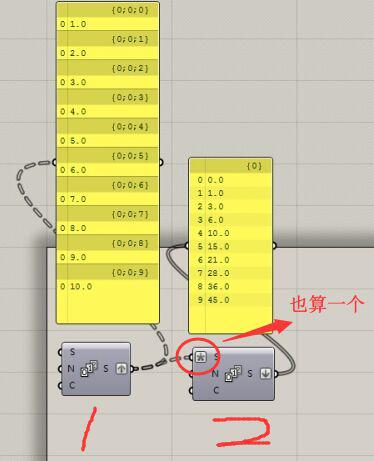
该答案用了两个Series套用，可见对树形数据的知识掌握的十分牢固。为了简化运算器数量，在第二个运算器输入端加了一个Expression表达式，该表达式也可以单独用Expression运算器做出，所以算三个运算器算出答案。那么学了Domain的知识以后，相信你们又有了一种解答方法啦：

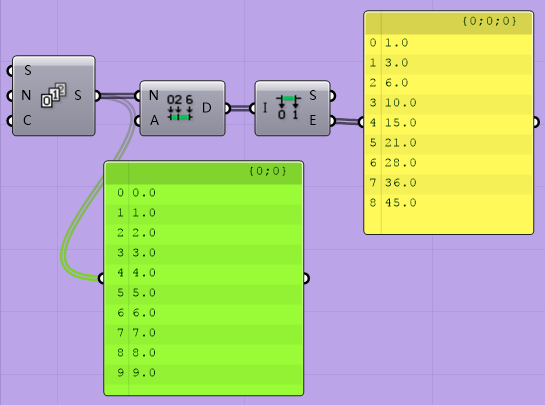
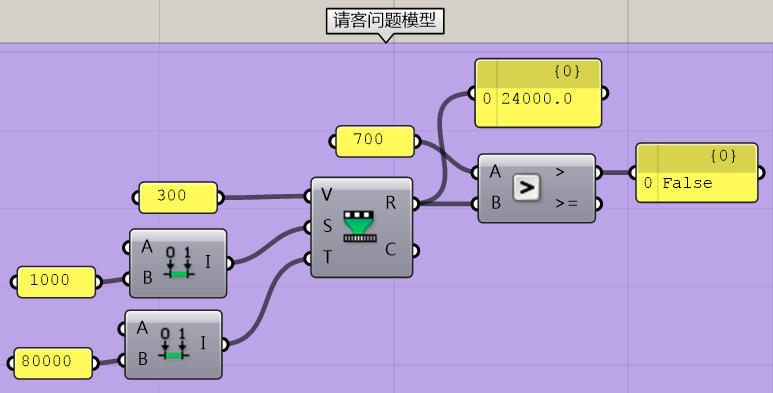
接下来我们要讲解Remap命令。我们在讲树形数据的级别时已经讲解过该运算器。它主要是用来根据原Domain中某数所处的位置，换算出新的Domain中该位置中的数字。通俗点讲，你一个月挣1000，请我吃了顿300的饭，我一个月挣八万，你来找我我请你吃了顿700的饭。你说咱俩谁够意思？怎么比较谁掏钱占得比重更大？这时候就是remap运算器的含义。该问题的程序如下：

接下来我们要讲大名鼎鼎的Divide Domain²啦。

关于它的作用，大家如果只看字面意思的话好像是把Domain²给分解了。但是大家可以很清楚看到输入端的U,V。实际上在设计中它主要是用来分割各种奇形怪状的表皮的。我们举个例子。

这是我在体育馆设计中设计的可以升起的屋顶。其中就运用到了我们的Divide Domain²运算器。

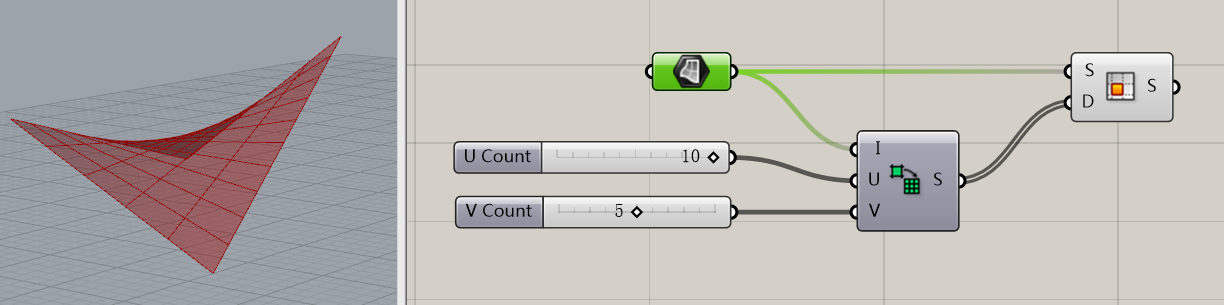
如图，我们需要将一个面来连接到输入端I。由于我们之前讲过Grasshopper的数据转化，这么人性化的Grasshopper会自动将我们输入的面转化为Domain²。然后我们在UV输入端输入要分割的数量，比如将整个U等分成十份，V等分成5份。这些分割过的Domain²共有10*5=50个，序号为0-49.其中红框内的运算器是List Length，即数据长度，专门用来查看数据共有多少项。

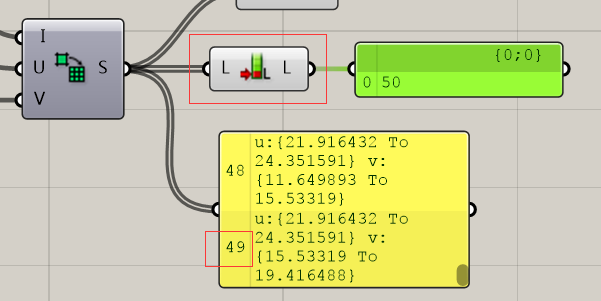
将这些运算器连入最右边的Isotrim运算器，即可将这整个曲面切成50个小曲面。Isotrim的用法就是根据输入端D输入的若干Domain²，将大的Domain²重新Trim（修建）成小的曲面。我们可以看到新输出的曲面个数为50个。

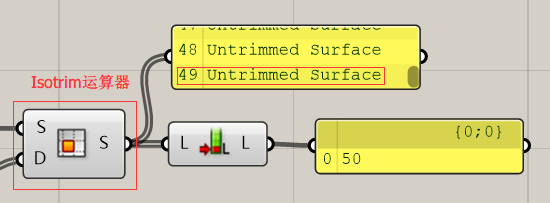
其中大家要注意，Isotrim输出的曲面均为未修建曲面。如果接触过犀牛的同学应该知道修剪过的曲面经常会发生一些很Bug的事儿，比如一旦重建UV（rebuild），曲面就会变成方正的原始曲面了。关于这个的原因我个人认为是因为修建只是系统判定在修剪后的Domain²下显示曲面，别的地方自动隐藏，有点类似PS蒙版的概念。一旦UV改变，就全部显示了。所以未修剪过的曲面是十分珍贵的呀！
接下来我们按照之前讲过的“Grasshopper建模逻辑翻译”的知识点，分析这个例子中我的屋顶下一步应该怎么做。很显然，应该每一个小曲面都偏移，并且偏移距离是一个随机的数据。那么我们应该主要用到偏移和随机两个运算器。最后我们根据结果定性定量进行修改，比如偏移不是我们要的方向，我们就在方向加上负号；我们按照需要的效果调整偏移距离，这是我们之前讲的第七步，也就是最后一步——调整。具体做法在初级篇中不再细讲，只把思路讲解到这里，大家领会思路即可。这是整个程序图：

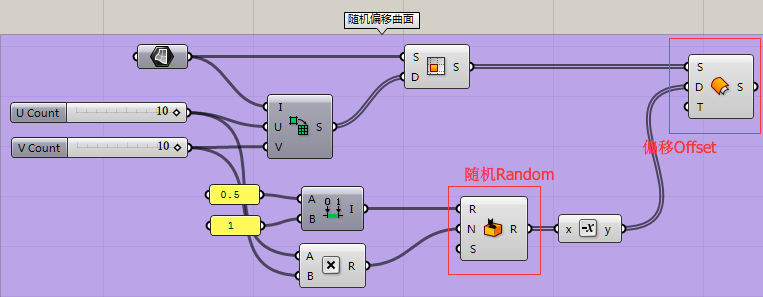
当然我们接下来可以加杆件，对曲面进行细化，同时根据采光要求将每个小面的大小也进行打乱渐变，对升起高度进行干扰渐变而非简单粗暴的随机。如何用一个简单的“原型（Prototype）程序”进行不断细化，是我们在提高班中主要要讲的内容。

OK，今天的内容讲的比较多。我们介绍了十几个运算器，然后又讲了一个小案例，可以说是比较丰富的。希望大家好好消化，可以用两次的时间来看这一篇帖子，确保自己学会且巩固了以后再进行之后的学习。Domain是非常重要的知识点，我们这里仅仅在最后给出了一个Domain和UV区间进行联立的案例，实际上在复杂的设计中这种操作十分常见。所以大家一定要掌握好Domain。

祝大家学业有成！
爱你们的小黄人君
DanielJin

 

初级12 Domain

 

———————————————————————————————————————————————————————

本文所有内容版权均属于作者所有

欢迎您扫描下方二维码关注小黄人君的微信公众账号